[lammps-users] Atom count in RDF calculations for a system of two types of polymer chains

LAMMPS LAMMPS Mailing List Mirror
1

Dear LAMMPS users:

I have this system of a polymer blend with two types of identical polymers (150 polymer A chains and 150 polymer B chains). All polymer chains are of equal size, consisting of 30 monomers each. I am trying to study the phase separation between them and was trying to calculate the radial distribution function for two cases: between polymers A and B and between polymers B and B.

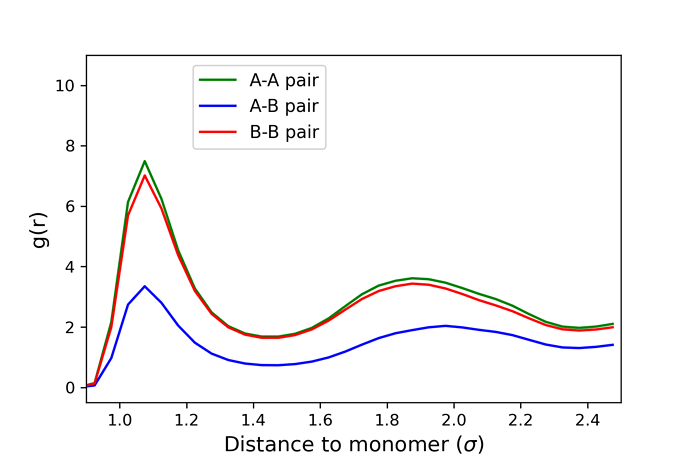
Phase separation is dictated by changing the epsilon parameter from the lj/cut command. For a system with epsilon set at 1.0 between polymer A and polymer B, I would expect to see thorough mixing between the polymers (as verified by visualization). However, upon plotting the RDF graphs, I see that the RDF values in the graph for B-B pairs (or even A-A pairs) is always approximately double that of A-B pair case, as shown in the picture attached with this email. Whereas a thorough mixing of polymers would have similar values on the RDF graph for both A-B and B-B pairs to show equal distribution of all atoms.

According to the “compute RDF” command from the website, it says that computing RDF involves the counting of both itypeN and jtypeN atoms. Now my question is this: when computing RDF for A-B pair, is LAMMPS counting both 150 polymer A and 150 polymer B chains (300 in total) and for the case of B-B pair, is LAMMPS counting only 150 polymer B chains? The results from A-A pair coincide with B-B pairs which could verify my suspicion about the atom count. Maybe that makes sense why RDF of B-B pair (or even A-A pair) has values that are approximately double than that of A-B pairs. Or I could be very mistaken in my rationale, thus decided to post here. Any suggestion on this matter would be highly appreciated!

For reference, all these simulations were done on the 26Jan2017 version, but I ran these on the relatively newer 3Mar2020 version but got the same results.

Thank you,
Shoumik
Stony Brook University, NY

rdf_compare_AA_AB_BB.png
rdf_compare_AA_AB_BB.png1800×1200 101 KB

2

First of all, the peak height of the g(r) doesn’t as easily translate into the number of neighbors as you might think. The g(r) is a relative probability and dependent on the number of possible pairs for a given number density. For translating the g(r) into the number of neighbors you have to look at the number integral (which is also computed by compute rdf).

Second, for molecular systems, you have to factor in the impact of excluded pairs due to 1-2, 1-3, and 1-4 exclusions based on your specia_bonds setting.
with the default (a weight of 0.0), those pairs are completely removed from the neighbor list and thus not available for compute rdf. Please see the corresponding note in the compute rdf docs.

Axel.