Hello,
I am wondering how the ‘Pure’ shear simulation of the periodic system can be performed with LAMMPS.
Below is the difference between ‘Simple’ and ‘Pure’ shear. In the case of pure shear, the orthogonal box should be diagonally skewed with constant side lengths.
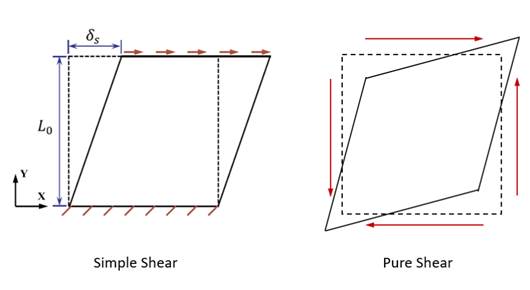
LAMMPS’ fix deform command with ‘xy or xz or yz’ parameter and constant volume ensemble simulates ‘Simple’ shear.
I would appreciate your thoughts and suggestions.
Thank you.
Sanjib



I am not sure but you may look addtorque command of lammps. Might it will help.




I think what you are asking for is implemented under the UEF package – see (for example) fix nvt/uef command — LAMMPS documentation . Hope the documentation gets you started!
All the best,
Shern




Not sure how the ‘addtorque’ will give such skewed diagonal deformation.
Currently, I am testing some options by applying velocity on four sides (assigning groups).
Thanks,
Sanjib




I have tested UEF. Both nvt/uef and npt/uef change box dimensions (lx, ly, lz) and make all tilt values (xy, xz, yz) non-zero.
I didn’t find any option in UEF to skew the model only in the XY plane while keeping this plane perpendicular to the Z-axis.
Thanks,
Sanjib




Please note that with fix npt/uef you can choose which dimensions are adjusted (same as with fix npt) and which not.
Please also note that the deformation that you describe in your figure cannot be directly realized in LAMMPS since the first axis of the box must always be the x-axis.
Thus you would need a more complex change to the box dimensions and tilt values and at the same time a remapping of the coordinates to have the same situation.
The documentation of fix npt/uef explains this. I don’t know enough about the details of this method to tell you what is required to exactly implement what you are looking for, but this is the only feature in LAMMPS that has the necessary functionality.




Hi Sanjib,
Is there a specific reason you want to apply pure shear by diagonally shearing your box instead of rotating your frame of reference by 45 degrees? Rotating would, of course, let you apply pure shear using fix deform or any of the non-uef deformation options by contracting one dimension while expanding another, preserving an orthogonal box. Although unlike UEF, this will still have the limitation that your box will become increasingly thin with strain.
Best,
Joel




Hi Joel,
I want to predict the shear stress-strain response of polymer considering large deformation with ReaxFF.
In the case of XY-plane shear, I want all stress components except XY-shear component zero. My understanding based on continuum mechanics only pure shear conditions will ensure this.
Are you saying – first rotate the orthogonal model by 45 degrees and then apply biaxial compression-tension using fix deform?
Thank you.
Sanjib




Hi Sanjib,
Yes, fix deform would be able to compress and expand two different box dimensions to apply pure shear:
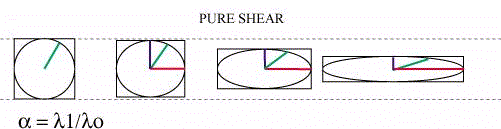
http://www.geosci.usyd.edu.au/users/prey/Teaching/ACSGT/EReports/eR.2002/Strain/STRAINd.htm
Best,
Joel




Hi Joel,
I have shown below the original and rotated box.

I have few queries –
-
What would be the orthogonal box dimensions of the rotated box?
-
How will the periodicity be maintained?
-
I have already tried bi-axial loading along the X- and Y-direction without rotating the model and it didn’t give any XY-shear, which is obvious. There is shear in the model in other oblique planes, but lammps doesn’t give oblique plane shear stress output. May I know why you think the rotated model will generate XY-shear stress under bi-axial loading?
Thank you.
Sanjib





Hi Sanjib,
Why not try fix nvt/uef with erate 0 ${some_rate}? From the documentation, that should give you an unchanged x-box-vector with yz-elongational flow.
You should look up “Kraynik-Reinelt boundary conditions” – this is the original method to achieve simulations of extensional flow for indefinite time with manageable box aspect ratios. Fix uef implements generalised KR BCs (which no longer has time periodic boxes, but accommodates arbitrary strain rates and vectors). All the references are in the documentation – I really encourage you to understand how the KR BCs work (even if you don’t fully understand the gKR BCs), because otherwise you will not understand the motivation (especially for the split-and-remap step) and you will not understand the problems with seemingly simpler approaches.
Cheers
Shern







![]()
![]()
![]()

