Dear developers,
I’m sorry that I ask some same questiones again. I think my last e-mail was not clear, so I did not get reply. Here I try to make my question as clear as possible, and I hope to get the help from everyone.
My system:
(1) I used the Kremer-Grest model, whose the data file can be found in BENCH folder in lammps (32000 monomers, chain length is 100).
(2) Before I imposed the shear, I clear the velocity of center-of mass (“velocity all zero linear”) and changed the box to be triclinic (“change_box all triclinic”).
(3) Then, I imposed the shear by “fix nvt/sllod” with “fix deform”:
fix 1 all nvt/sllod temp 1.0 1.0 1.0 tchain 1
fix 2 all deform 1 xy erate 0.001 units box remap v
My qusetions:
(1) Is momentum conservation true?
Lammps user manual cites the work of P. J. Daivis and B. D. Todd (J. Chem. Physics, 124, 194103 (2006)), they discussed the momentum conservation in part IV. I think they expressed the finite precision numerics leads to an inherent instability in elongation, and no such problem occurs in shear flow.
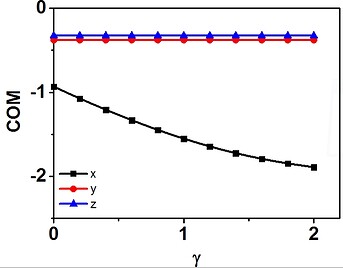
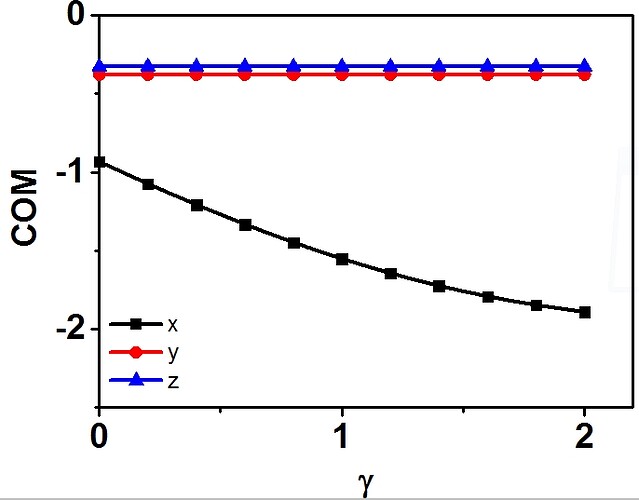
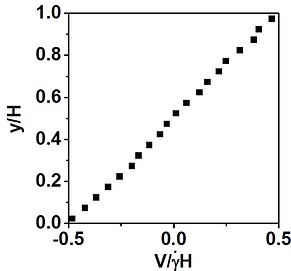
However, I checked the center-of-mass of the system (“compute 1 all com”), and the result shows the system moves in x direction (see below, the ordinate the is the center-of-mass coordinate in three direction, and the abscissa is the strain).
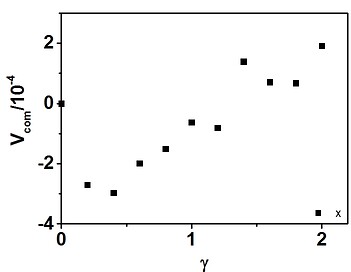
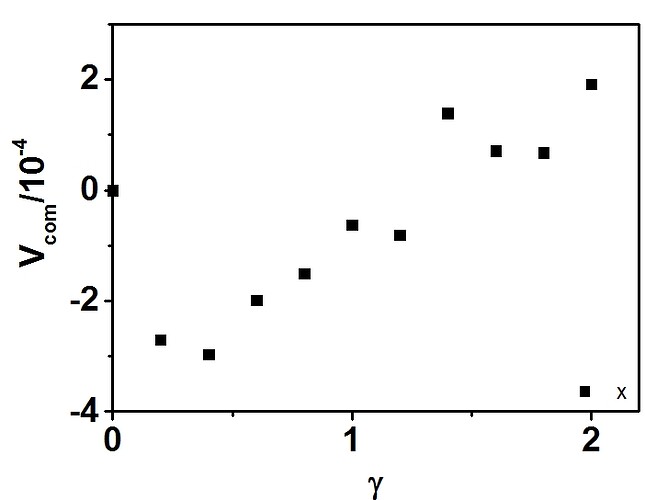
I also dumped the velocity of atom (dump command), and calculated the velocity of center-of-mass in x direction (see below), which also shows the momentum is not conservation. The velocities are zero [~O(1E-15)] in y and z direction.
So, is it true when I use the sllod method, or did I miss something in user manual?
In fact, I followed the previous work of P. J. Daivis and B. D. Todd (J. Chem. Phys. 97, 616 (1992)), they states: “In very long simulation runs, numerical drift caused by truncation and discretization errors (in both the computer and numerical differential equation solver), usually leads to some slow drift in the values of the constrained variables.” Thus, is my obervation caused by numerical drift ?
(2) Is the velocity field always linear?
Altough the SLLOD suppose the velociy filed is linear, is it possible that we will get non-linear velocity filed in some systemes and conditions?
Best wishes,
Yongjin Ruan