[lammps-users] What is the center-of-mass velocity when I use the sllod command?

[yjruan]

Dear developers,
I worked on the Kremer-Grest model (bead-spring model: LJ potential with FENE potential, which can be found in BENCH folder in lammps), and I imposed the shear by “fix nvt/sllod” with “fix deform”:

fix 1 all nvt/sllod temp 1.0 1.0 1.0 tchain 1
fix 2 all deform 1 xy erate ${Rate} units box remap v

For some reasones, I check the center-of-mass velocity by velocity file (i.e. dump ID all custom {Step} {name} id vx vy vz).

However, I found the center-of-mass velocity (in flow direction) increases with strain. And the velocity in other direction is zero [~O(1E-14)]
For one sample, I got:

[Steve_Plimpton1]

In LAMMPS, shearing in xy with SLLOD will impose a net x-direction velocity on the system.
I.e. atoms at the lower face will be (near) zero velocity. Atoms at the upper face will have a large
velocity. So the ave velocity will be 1/2 the upper face velocity.

Steve

[yjruan]

Hello Steve,
Thanks for your reply!
In fact, I have made a new test about this problem. More results can be found in the e-mail (2021-05-13) “Two problems when we use the nvt/sllod command in Lammps.” and the latter reply.
I make it shortly.

(1) I used the Kremer-Grest model, whose the data file can be found in BENCH folder in lammps (32000 monomers, chain length is 100).
(2) Before I imposed the shear, I clear the velocity of center-of mass (“velocity all zero linear”) and changed the box to be triclinic (“change_box all triclinic”).
(3) Then, I imposed the shear by “fix nvt/sllod” with “fix deform”:
fix 1 all nvt/sllod temp 1.0 1.0 1.0 tchain 1
fix 2 all deform 1 xy erate 0.001 units box remap v

Note: shear rate is 0.001

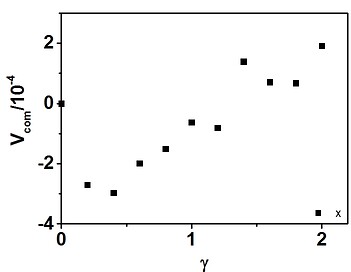
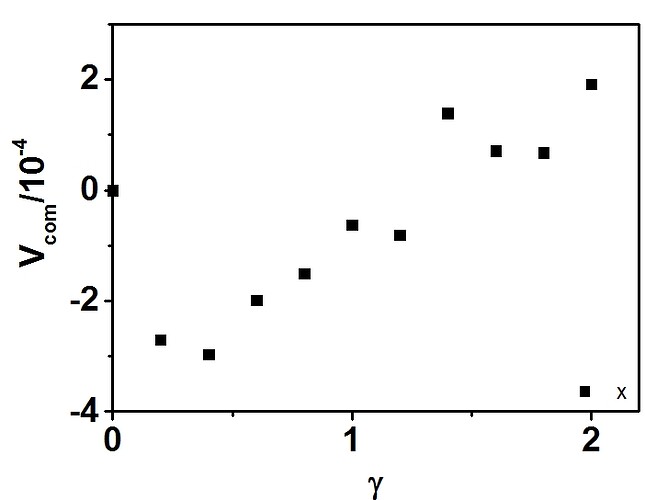
First, I have shown that the velocity of center of mass increases with the strain. In other words, the velocity of center of mass is not a constant.

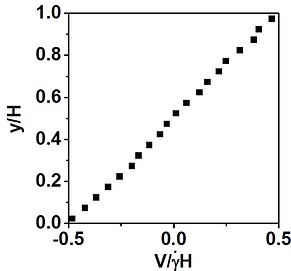
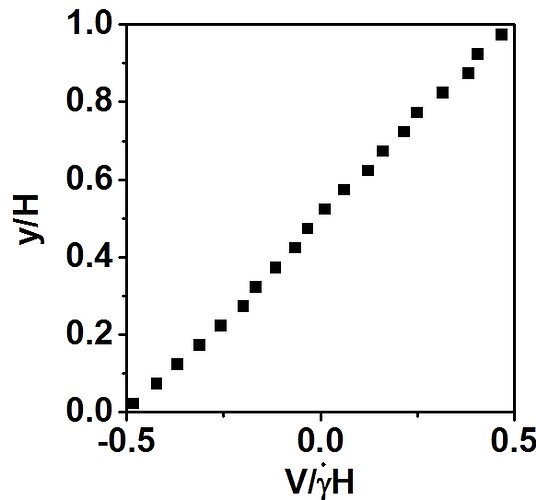
Second, Axel tell me using the following command to get the velocity profile:

compute ybins all chunk/atom bin/1d y lower 0.05 units reduced
fix 5 all ave/chunk 40 5000 200000 ybins vx file yprof.dat

The results is shown in below, which states the velocity is range from -V/2 to V/2. Thus, the COM velocity should be zero, not V_max/2.

Third, I read the fix deform.cpp as possible as I can (I am much more familiar with Fortran). I think if the box is [0, H_y]，we can get “atoms at the lower face will be (near) zero velocity. Atoms at the upper face will have a large
velocity.” However, my box is [-H_y/2, H_y/2]

If possible, you can tell me what I can do, I will try my best to check it.

Sincererly,Yongjin Ruan

[Steve_Plimpton1]

I think you are probably making measurements too soon for a non-equilibrated system.
The fact that some atoms (chains) are flowing backward is an indication of that.
Here are a few suggestions.

a) Visualize your system. See the movie for NEMD box deformation at this link:

https://lammps.sandia.gov/movies.html#viscosity

If you look at an xy projection (down the z axis) of your 3d system, that is what
fix deform xy should look like. I suggest coloring the monomers by their molecule ID.
Then it will be easy to see what is going on. Note that the particles are flowing with the box.

That is what fix nvt/sllod pushes the system towards, but it can take a while to get there.
Note that the top of the box moves to the right, then when it reaches a max tilt it
flips to a negative tilt (w/out moving atoms) and that continues forever if you run long enough.
The key point is that when the system is equilibrated, the entire fluid is moving in sync with the box.
Until that happens you are not in equilibrium. That is why I said the particles at the
bottom should have a tiny +x velocity (on average). The ones at the top should have
a large +x velocity. It doesn’t matter what your box dimensions are (0 to L vs -L/2 to +L/2).
The lower y edge (xz face in 3d) should remain motionless, the top y face should move
fastest.

b) When in equilibrium, the average Vcom for the system should thus be a constant. It should
be half of the speed the top box face is moving at. So it is a function only of the strain rate, not of the strain itself.
Over a long simulation with many flips the strain simply grows larger and larger. It’s not possible
that in equilibrium that Vcom grows with strain or it could become infinite.

c) If you start with a system with Vcom = 0, it can’t instantly acquire the necessary Vcom final just because the box deforms.
The box exerts no direct force on the fluid. The SLLOD thermostat does, but slowly.
You can help the system equilibrate more quickly by assigning an initial x velocity to the
atoms (superposed on their thermal velocity) which is consistent with the box shear. The
velocity ramp command can do that. I.e. assign an extra zero x velocity to particles at the y bottom
and a Vtop x velocity at particles at the y top and ramp it in between. Thus Vcom initial = desired Vcom final.

d) For an entangled polymer melt with long chains (like the benchmark, the chains are quite long), it
cannot shear nicely with too large a strain rate and ever flow smoothly. Because of the entanglements.
You’ll have to expt to see what that limit it. Likewise expt with what the SLLOD time constant is.
I suggest you start with a LJ fluid, then short chains, then this longer chain system.

Steve