Hi Alex,
You are right. Its not a simple cubic unit cell. I erased the other atoms
in the image to reduce the complexity of the Question. In principal, the
question is how can a substitution or a vacancy be created using the LAMMPS
command, lattice custom 1 a1 1 0 0 a2 0 1 0 a3 0 0 1 basis 0 0 0
SG
Hi Alex,
You are right. Its not a simple cubic unit cell. I erased the other atoms
in the image to reduce the complexity of the Question.
it is irrelevant. the atom on the corner of a (cubic) cell, is shared
with 8 cells and thus you cannot have two of those atoms be different. this
is crystallography 101.
In principal, the question is how can a substitution or a vacancy be
created using the LAMMPS command, lattice custom 1 a1 1 0 0 a2 0 1 0 a3 0 0
1 basis 0 0 0
sure you can have vacancies, but not in the way you require it. nobody can
suggest you LAMMPS input commands for an ill-defined crystal structure.
axel.

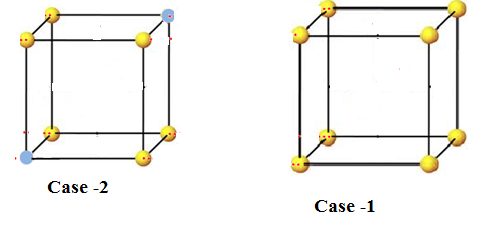
Ok, I reframe my question,
How can I specify the black atoms in the BCC lattice (shown below) using LAMMPS command? This is from a published paper (doi:10.1016/j.actamat.2005.09.034)

Ok, I reframe my question,
How can I specify the black atoms in the BCC lattice (shown below) using
LAMMPS command? This is from a published paper
(doi:10.1016/j.actamat.2005.09.034)
by providing their respective "basis" entries with the respective
fractional coordinates.


Ok …
How about defining a custom lattice using primitive lattices vectors <a 0 0 > < 0 a 0 > and <0 0 a> (where “a” is the lattice constants) … Then input all the atoms using Basis option :
Base1 a 0 0
Base2 0 a 0
base 3 0 0 a
base 4: a a a
base 5: 0 a a
base6: a 0 a
base7: a a 0
base8: 0 0 0
base9 a/2 a/2 a/2
base10 a/2 0 0
base11 a/2 a/2 a
^_____^ This should Work … Actually i will try to do it , and this is a good exercise for a UnderGrad student learning 101 Crystalography …
Oscar G.


You don’t “create” a vacancy. There is simply no atom there.
Since the unit cell is replicated, you can’t put any atoms in
the basis set which have fractional coord of 1 in any of
the 3 dimensions. I.e. the basis set for the cube
you’ve drawn is 1 atom, not 8. The replication creates
the other 7 atoms, in other images of the unit cell.
Steve




