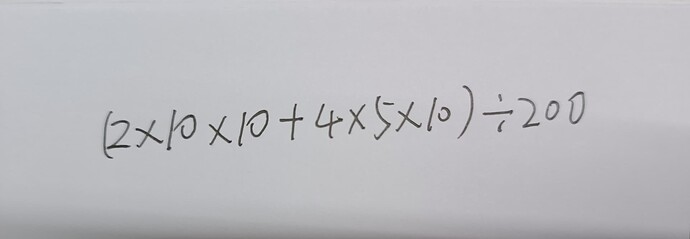Hello LAMMPS community,
I am trying to implement a Non-Reflective (a.k.a Pressure-Transmitting) Boundary conditions for a shock wave (i.e. so the wave is not reflected from the material/vacuum interface) in a spherical geometry similar to those described in Phys. Rev. B 96, 205429 (2017) - Mechanism of single-pulse ablative generation of laser-induced periodic surface structures. I’m thinking of using existing LAMMPS Langevin fix which operates with a radial component of atomic velocity in the boundary region. The manual suggests that I can use fix_modify to change the velocity the Langevin fix uses in order to feed it a radial component of velocity I get from compute. However, the compute command doesn’t seem to allow me to operate with velocities. Is there any workaround?
Thank you!
Your description is too vague and thus not easy to follow. For example it is not at all clear what you mean by “radial component of velocity”.
Can you produce a small test input with simple LJ particles that would demonstrate what you are trying to do? Or at least create some kind of sketch/diagram that would illustrate what your system is and what you want to do with it?
Hi Axel,
Thank you for your response. I’ve attached a scheme for the experiment. Basically, it’s a sphere of liquid argon with a stress generation region in the vicinity of its center. For now, I simply use velocity distribution for stress generation. As the stress wave approaches the boundary, it should be suppressed by Non-Reflective Boundary conditions so it doesn’t reflect back (that’s my goal of using NRB, basically). I am planning to implement the NRB with the Langevin thermostat using the equations shown in the picture. For this purpose, I need to operate with radial component of velocity.
NRB_Sphertical_Scheme.tif (3.2 MB)
The documentation says that the fix_modify option for fix langevin works by passing it an appropriate temperature compute. I am guessing you want to calculate a temperature based purely on motion components transverse to the radial motion. None of the existing compute temp/X styles do that. So you would have to write your own in C++, paying attention to all the “bias” methods that remove the local peculiar velocity before thermostatting and then add them back in afterwards.
Alternatively: if you can express the desired x, y, and z components of your additional forces as per-atom variables – which can depend on an atom’s instantaneous position, velocity, etc. – then fix addforce will let you brute-force add those forces to the atoms at every step.
For example, here’s a first stab at a Langevin thermostat which purely thermostats the velocity component along the x=y axis:
variable gamma equal 0.783 # a random number
variable eta equal 6.60123 # a random number
variable vxy atom vx/sqrt(2)+vy/sqrt(2) # the transverse component is vx/sqrt(2)-vy/sqrt(2)
variable fxy atom -v_gamma*v_vxy + v_eta*normal(0,1,150923)
fix manual_langevin_thermostat all addforce v_fxy v_fxy 0
Hi srtee,
Your response was really helpful!
In your implementation of the Langevin thermostat, you use a normal distribution to account for the random force. However, your eta parameter doesn’t seem to correlate with your sigma = 1. Is that intentional?
I also have a follow-up question. If you use a manual fix to update forces, how do you control how often you update your manual_langevin_thermostat? In langevin fix it is controlled by damp parameter.
My earlier code example is just meant to demonstrate what can be done in LAMMPS. The numbers in it were chosen completely from thin air and are very unlikely to be correct by chance.
The Langevin damping factor is something you have to determine based on the science of your system. The simulation will likely run for any value of the damping but whether it is physical or not you have to work out for yourself. The damping factor, very roughly, controls the time scale on which the temperature of your system fluctuates, and it is up to you to work out what that would be for your simulation to match up well with your desired physics.
In addition, for a Langevin thermostat, the frictional coefficient and random force amplitude need to obey the Fluctuation Dissipation theorem. This is taken care of in the code for fix langevin, but if you were making your own via calculating and adding the forces manually you would have to ensure that the statistics and thermodynamics are correct.
Hi, I’ve been trying to use this non-reflective boundary condition lately. Have you solved it yet? Is that the command you used, fix vicious? I’m looking forward to hearing from you
Hi @XuXinNian ,
The fix viscous command adds a viscous term that will cause your system to have an energy leak. What you may want to try is to compute the center of mass (CoM) velocity for atoms in the NRB region and apply viscous force to every atom in this region based on the CoM velocity. As srtee mentioned above, the most straightforward way to implement this is to use the addforce fix.
Thank you very much for your answer. I seem to understand
Sa is defined as the total area of the boundary divided by the number of boundary atoms.
I’m a little confused about this sentence, can you help me to answer it? Let’s assume that the laser is in the x direction. In the boundary conditions, the distance in the x direction is 0-5 emm, and the distance in the y and z directions is 0-10 emm, with 200 atoms. How his Sa was calculated. Is it (21010+4510) /200? Or some other algorithm?
Hello, I am trying to calculate the NRB using the following two methods, but every time I run it, it stops at the first step and doesn’t move any further. Is this because I have a problem with my boundary velocity, which I set to the average velocity (center-of-mass velocity) of all atoms within the boundary? Can you help me with this?
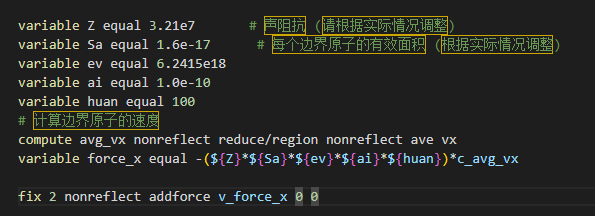
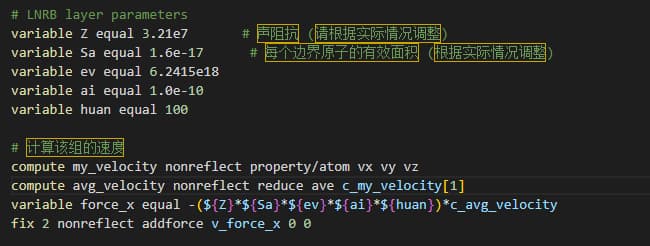
Please start a new topic – your current problem doesn’t have much to do with the previous posts in this thread.
When you do start your new topic please include the full input script that you used. It is impossible to tell what the problem is based on the small section you posted.
Please also refrain from attaching screenshots. Instead, please paste your script in as plain text. You can use backticks
```
like this
```
to ensure that special characters in the script do not mess up the forum post formatting.