Hi
I am running a DPD simulation for a water/surfactant system in order to calculate the critical micelle concentration.
I am trying to calculate the pressure; I have to run my simulation at the normal pressure.
I am using LJ units, the simulation density is three, the degree of coarse graining is five, and water is taken as my reference molecule for the calculation of the volume of one bead (150 angstrom for 5 water molecule). The cut-off distance is 0.766 nm using the above information and the following equation
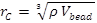
image001.emz (1.58 KB)
Hi
I am running a DPD simulation for a water/surfactant system in order to
calculate the critical micelle concentration.
I am trying to calculate the pressure; I have to run my simulation at the
normal pressure.
I am using LJ units, the simulation density is three, the degree of coarse
graining is five, and water is taken as my reference molecule for the
calculation of the volume of one bead (150 angstrom for 5 water molecule).
The cut-off distance is 0.766 nm using the above information and the
following equation
[image: r_C=∛(〖ρ V〗_bead )]
What I understand, is that T = 1 in LJ unit is equivalent to 300 K, this
makes the epsilon equals to (KB *T= 4.1E-21 Joule).
If all these calculations are correct, then using the cut-off distance
along with the epsilon, the normal pressure should be 0.011 in LJ units. Is
that right?
no. T *depends* on epsilon. if you want T in "real" units, you have to
know the "real" epsilon first.
if you want to have a direct correlation to specific properties of specific
materials in real (i.e. non-reduced) units, why do you go through the
complication of using reduced (or lj) units in the first place?
axel.
![]()