"Pair distance < table inner cutoff" error using soft core potential

LAMMPS LAMMPS Mailing List Mirror
1

Hi all,

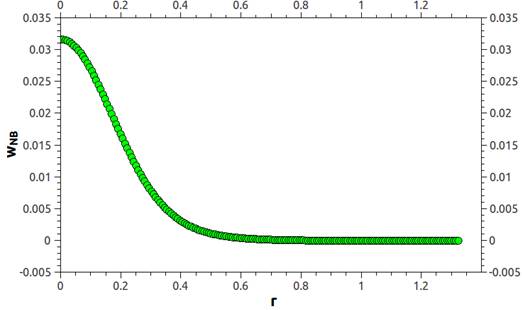
i wish somebody can help on that one. I’m trying to run DPD simulations of coarse-grained polymer chains. I’m using pair_style table and bond_style table commands in order to define the conservative force and pair_style dpd/tstat to thermostat my system. The tabulated values for bonded and non-bonded interactions were taken from the potential of mean force obtained after performing MD simulation at the coarsed-grained level under study. In order to combine pair_style table and dpd/tstat, i’m using pair_style hybrid/overlay. Following the tips given by LAMMPS documentation, i started by using linear interpolation on pair_style table, i matched the N of the pair_style equal to the tabulated N, and i tried to use pair_write command in order to produce a plot of what the final interpolated potential looks like but without succeeding (i get an error saying “Pair style does not support pair_write”. Is there any way to solve this issue?). Since DPD uses soft potentials, beads can overlap, so my potentials inner cutoff is very close to zero value (if i use an inner cutoff of zero, LAMMPS though me an error saying “Invalid pair table cutoff”). So, after running my simulation, everything seems to be fine, but after several thousand steps i get and error saying “Pair distance < table inner cutoff”. Coincidence or not, I realized that this error appears just before the simulation reaches the target temperature. What i realize about this error is that particles moved to close, to a distance lesser than what the table can afford. Below i show how the non-bonded potential in LJ units i’m using looks like (it was taken from Guerrault X, Rousseau B, Farago J, J. Chem. Phys. 121, 13, 6538-6546 ), and also parts of my table file:

unknown-EIF8WV.png
PMF_PE_NB
N 181 RSQ 0.00001 1.32159

1 0.00001 0.03166 0.00000
2 0.00734 0.03163 -0.07680
3 0.01468 0.03155 -0.15316
…
179 1.30690 0.00000 0.00000
180 1.31424 0.00000 0.00000
181 1.32159 0.00000 0.00000

I wonder if anybody can give me any tip or advise on how i can solve this “Pair distance < table inner cutoff” issue.

Thanks so much for the time.

Many regards

Sacha

2

Re: seeing your table fitting with pair write. I think the
problem is that you are using a hybrid style with dpd/thermostat/
Since all you care about is the tabluated portion, just use
an input script w/out pair hybrid and only the tabulated potential.
Run for 0 steps and use pair_write, just as a check that the
tabulation looks like you expect.

I can’t recall why pair table doesn’t allow an inner cutoff of 0.0.
Maybe it has to do with a derivative at the end point. Paul,
can you remember why this is a restriction?

If you use epsilon for the inner cutoff (e.g. 1.0e-6), I’d be
surprised if you ever got two particles to overlap within
that distance. That seems unlikely, unless your model
is collapsing to have particles exactly on top of each other.
I suppose that could happen if your potential actually had
a minimum at r = 0, which I presume it shouldn’t.

Steve

unknown-EIF8WV.png

3

An inner cutoff of zero is not allowed in pair table since that would result in some divide by zero problems. Tabulated forces are stored as f/r, where r is the interatomic distance. In designing the pair table style we did not have in mind pair potentials that allow particles to overlap. Even so, I agree with Steve’s suggestion that by using a really small inner cutoff, you shouldn’t ever see exact particle overlaps unless they are placed there intentionally or possibly if there is a minimum in the potential that pushes them to exact overlap. You might try an even smaller but positive inner cutoff.

Note that pair style dpd skips interactions where r < 1e-10, apparently to avoid similar divide by zero issues:

#define EPSILON 1.0e-10

if (r < EPSILON) continue; // r can be 0.0 in DPD systems

rinv = 1.0/r;

Paul

image002.jpg

4

Dear Paul and Steve,

appreciate so much for the tip. I decreased even more the inner cutoff
value and everything seems to run smoothly.

All the best,

Sacha