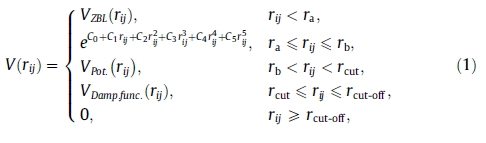Pair potential hybrid

[_hossain_khan_via_Go]

Dear LAMMPS user

I am trying to follow one journal where potential is complicated to me. I have written my way. Still, it needs several improvements. Can anyone help me with it? Any kind of suggestion would be helpful for me.

echo both
units metal # set ‘metal’ units (Angstrom,ps timescale)
dimension 3
boundary p p p # periodic BCs
atom_style charge

neighbor 2.0 bin
neigh_modify delay 0 every 1 check yes # neighbor command modifies potential’s natural cutoff_needed?

----------------------- ATOM DEFINITION ----------------------------

read_data Fe_Fe3O4_center.lmp

write_dump all atom sinusoid_4.lammpstrj

--------------- Creat Atoms / Geometry -----------------------

mass 1 55.847
mass 2 15.999
region rPKA sphere 52.127 52.127 104.255 .1 # Create spherical region ‘rpka’ at x, y, x with radius

------------------Define Interatomic Potential -----------------

pair_style hybrid/overlay zbl 0.5 7.4 eam/fs morse 2.5 buck 2.5 coul/dsf 0.15 15

pair_coeff 1 1 zbl 26.0 26.0
pair_coeff 1 2 zbl 26.0 8.0
pair_coeff 2 2 zbl 8.0 8.0
pair_coeff * * eam/fs Fe_2.eam.fs Fe Fe

pair_coeff 1 2 morse 0.3 2.0 2.5
pair_coeff 2 2 buck 22764.3 0.1490 20.4
pair_coeff * * coul/dsf

Below, I have given the potential form and table for pair coefficient.

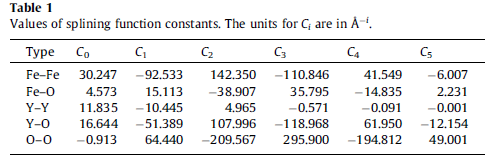
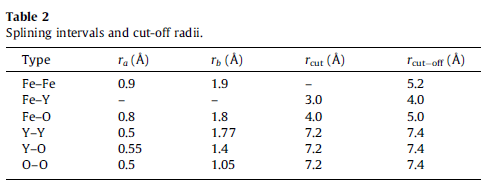
All the interactions between different types of atoms are described using interatomic potentials. All potentials are splined to the ZBL screened Coulomb potential, for close particle separation, using a sixth order exponential polynomial. They are then smoothly truncated to zero at a distance rcut-off. The form of the pair potentials used is given in the following equation :

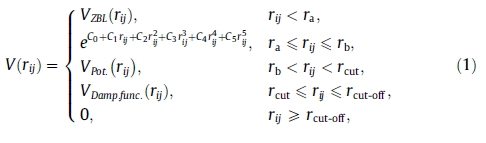
where rij is the atomic separation, C0–C5 are splining constants, VPot. and VDamp.func. are interatomic potentials and smooth damping functions respectively. The distances ra, rb, rcut, rcut-off are the active ranges for the given expressions. All these values depend on the types of interacting atoms. Values for the constants are given in Table 1. Splining constants were chosen to give a smooth join between VZBL and the sum of VPot. and the Coulomb energy by making V(rij) and its first two derivatives continuous.

[akohlmey]

Dear LAMMPS user

I am trying to follow one journal where potential is complicated to me. I
have written my way. Still, it needs several improvements.

​it not only needs improvements, it is very wrong and needs to be done
differently.​

Can anyone help me with it? Any kind of suggestion would be helpful for me.

​you need more help than what the mailing list can provide you with.
specifically, you need help understanding the difference of what you did
(which looks like you just combined more-or-less randomly guessed stuff)
and what the paper describes. that is something you need to discuss with
your adviser, who is responsible to training you (or finding somebody
sufficiently competent​ to train you).

​with pair style hybrid/overlay, you are *adding* terms to the interactions
(from r=0 to r=r_cut). however, the potential you show below is a
*piecewise* defined potential, where only one term at a time is active. you
cannot model that with hybrid/overlay. even if you could, your overlay
model makes no sense at all. you apply zbl to *all* interactions *and* the
iron EAM interaction *and* the coul/dsf term.

to make this interaction model work with LAMMPS you have to either
implement this as a custom new pair style or use tabulation with pair style
table (which can be tricky, especially for such a complex interaction
model).​ i cannot say which, because there are still important details
missing. it is pointless to discuss this here at the moment for the reason
given above. talk to your adviser and get help with understanding a
piecewise defined potentials vs. regular potentials.

​axel.​