Dear All,
Please excuse my simple question. I am trying to understand how Lammps calculates pairwise forces for a non-bonded periodic system based on the theory described in the paper titled “General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions” A. P. Thompson, S. J. Plimpton, W. Mattson, J Chem Phys, 131, 154107 (2009).
Please see the figured attached:
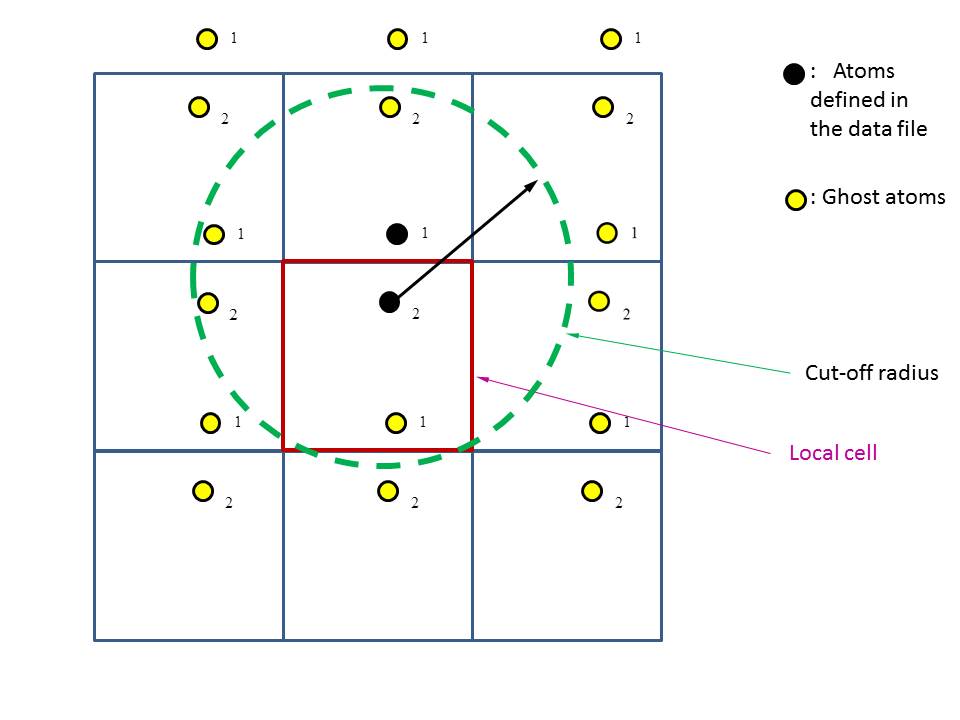
(1) I have one 2-non-bonded-atom system (atom 1 is outside of the local cell) under periodic condition.
(2) If I want to calculate force on atom2, with some specific cut-off (I know the cut-off shown is too large for a real simulation).
(3) Does Lammps consider all (5 atoms in the figure) atoms within the cut-off radius to calculate the force on atom 2?
Thank you for your explanation and help,
Lili
Dear All,
Please excuse my simple question. I am trying to understand how Lammps calculates pairwise forces for a non-bonded periodic system based on the theory described in the paper titled “General formulation of pressure and stress tensor for arbitrary many-body interaction potentials under periodic boundary conditions” A. P. Thompson, S. J. Plimpton, W. Mattson, J Chem Phys, 131, 154107 (2009).
Please see the figured attached:
(1) I have one 2-non-bonded-atom system (atom 1 is outside of the local cell) under periodic condition.
(2) If I want to calculate force on atom2, with some specific cut-off (I know the cut-off shown is too large for a real simulation).
(3) Does Lammps consider all (5 atoms in the figure) atoms within the cut-off radius to calculate the force on atom 2?
That can be extremely easily found out by constructing an input for such a system and looking at the neighbor list statistics after a “run 0”
I am also certain that this topic has been discussed numerous times on this mailing list and thus there should be a more detailed explanation in the archives. Please do have a look, too.
For any I,J interaction between a pair of atoms,
it will be stored in the neighbor list exactly once,
and thus computed exactly once.
Steve
