Dear all,
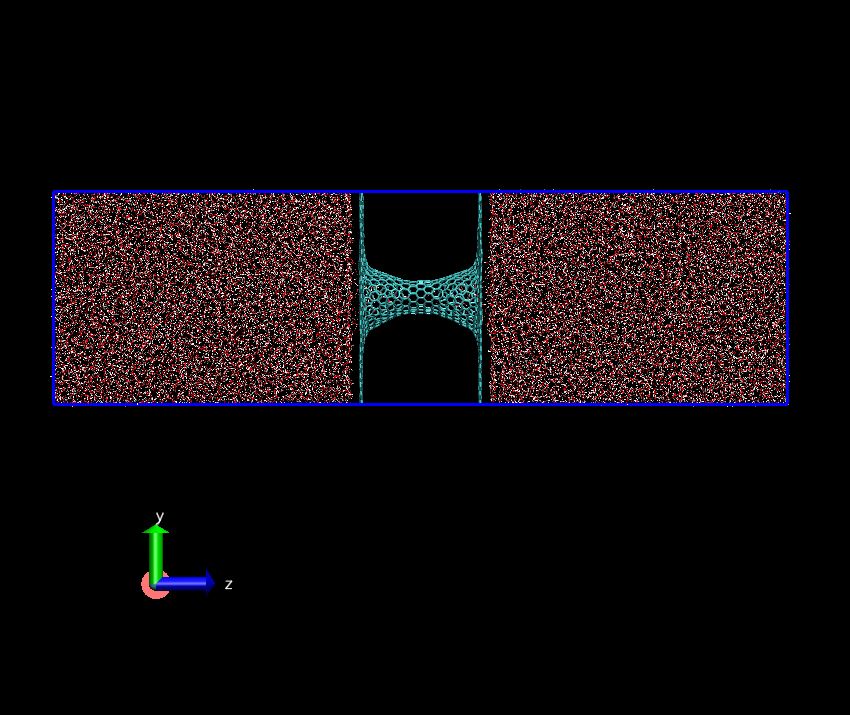
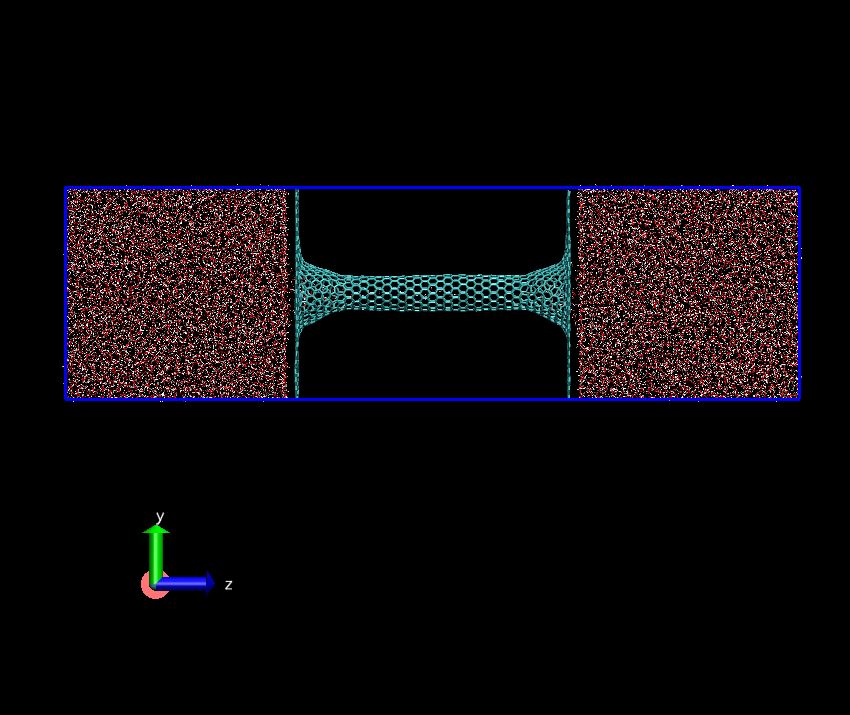
I am not sure if it is appropriate to post it here. I am trying to simulate a water flow through a nano-channel. Attached please see the system I am modeling. Nano-channel aligns in the z-direction connecting holes of two graphene membrane which lies in the x-y plane. Different lengths of nano-channels are considered, while the dimensions of simulation box are fixed (5.922nm, 5.8614nm, 20nm in x, y, z directions)
The pressure gradient is applied by artificially adding acceleration/force on each water molecules in the z-direction. I would like to investigate the water flow rate across different nano-channel under the same pressure drop.
However, I am confused about the relation between the pressure drop and atomic acceleration/force. It is different in literature about how to calculate them. There are three different ways as below:
-
(Acceleration)*(Density)=(Pressure drop)/(Length)
Length here is the length of nano-channel
-
(Acceleration)*(Density)=(Pressure drop)/(Length)
Length here is the dimension of simulation box in the z-direction.
-
(Force)(Number of water molecules)=(Pressure drop)(Area of simulation box in the xy-direction)
In my simulations, the second method is used to calculate the atomic acceleration. The pressure drop is fixed at 200MPa. The results are hard to understand. The water flow rate increases with the length of the nano-channel. However, in the Poiseuille flow, the flow rate should be proportional to the 1/(the length of the nano-channel).
Could you please help me to understand my results? Which method is correct to calculate the atomic acceleration by the setting pressure drop?
Thank you very much for your attention. I would appreciate it if you have any comments.
Best,
Jason
Dear all,
I am not sure if it is appropriate to post it here.
you would be better off to discuss your question with your
adviser/supervisor/PI/colleagues/collaborators and/or post in a forum that
focuses on science and not on a specific software. there isn't really
anything pertaining to LAMMPS in your description below. if you get *very*
lucky, there is a subscriber that has that kind of experience you are
looking for, but that is quite unlikely.
axel.


Axel is correct. You really should ask for help and feedback from your teachers and/or collaborators before continuing. These questions have nothing to do with LAMMPS.
For what it’s worth, here are my comments:
Firstly, I’m not sure how acceleration is relevant to calculate the flow rate. Isn’t flow rate a steady-state quantity? (Consequently, I do not understand the relevance of the first two formulas you listed.) Before measuring the flow rate, I would wait until the velocity of particles located at the center of the tube is constant (not increasing or oscillating over time).
It was helpful that you posted pictures of your system. After looking at your pictures. I think you should also avoid having empty space in the center of the tube when you calculate the flow-rate. Surface-tension will complicate estimation of the pressure. (Surface-tension causes capillary pressure.) In general it’s probably better to avoid any gas-liquid interfaces in your system. (Ideally, there should be no bubbles, or gas-liquid boundaries on either side.)
I suggest that you fill the tube with liquid, and wait for the pressure equilibrate, apply force to the atoms (using fix addforce, for example), and wait for steady-state flow. (Perhaps you are already doing this.) Otherwise, all kinds of strange things can happen.
Eventually, you may also need to use longer tubes. Otherwise it is difficult to estimate the effective length of the tube, because the tube diameter is not uniform at the ends. (Very nice-looking tube junctions, by the way.)
You will get better advice from your own teachers.
Good luck
Andrew


Dear Andrew,
Thank you very much for replies from you and Axel. Sorry for my late response. I had a meeting this afternoon.
I agree you and Axel. I should have discussed with my teachers first.
If you are interested, I would like to explain a little bit the method I used to generate water flow In my simulations. I applied forces on each atoms to assign them a fixed acceleration. In this way, I can mimic the pressure drop on the channel. The method is following the some posts (by Steve, Laurent) in LAMMPS mailist.
http://lammps.sandia.gov/threads/msg05593.html
http://lammps.sandia.gov/threads/msg21420.html
http://lammps.sandia.gov/threads/msg10736.html
Actually, I meant to ask how to calculate the mimicking pressure drop if I apply forces on each water molecules. So I posted three ways to calculate it in my first letter. But I am not sure which one is correct. I will look for literature about this.
I really appreciate that you gave me some suggestions. The below is some explanation of your comments. Please skip it if you are not interested in.
- Isn’t flow rate a steady-state quantity?
Yes. The flow rate is calculated after I apply atomic forces for a long time. It is not increasing or oscillating over time.
- I think you should also avoid having empty space in the center of the tube when you calculate the flow-rate.
Actually, there is a mono-water chain in the center of the tube. The index of the middle tube is (12,0). The water molecules are tiny. I am sorry the image is not clear enough to see them.
- it is difficult to estimate the effective length of the tube.
Yes, I agree with you. My goal is to investigate the geometry influence on the flow rate. I set up this hourglass-shape channel on purpose. The size and angle of the opening inlet and outlet are also parameters I am interested in. It is reported that the opening structures can facilitate the flow rate. I tried 7 cases in which the opening structures are the same but the total lengths of channels are different. I only show two structures of them in my first letter.
Thanks again for your help and advises.
Best,
Jason


Dear Jason,
Applying a constant force to all water molecules as you do mimics a gravity-induced flow. In a homogeneous system the relation to a pressure-drop-induced flow is trivial, but in a heterogeneous system as the one you consider here it is less obvious. In a recent paper, where we considered systems very similar to yours, we chose a different approach, namely imposing the pressure in each reservoir with two pistons:
http://scitation.aip.org/content/aip/journal/jcp/141/18/10.1063/1.4897253
As for the effect of the tube length on the flow rate, it is not obvious at all. Friction in nanotubes being extremely small, viscous dissipation is localized at the entrances, and the length of the tube will only have an indirect effect, by (slightly) modifying viscous dissipation at the entrances…
Best regards,
Laurent


if you get very lucky, there is a subscriber that has that kind of experience you are looking for,
Jason - you got very lucky. Laurent has modeled the exact kind
of issues you are interested in! His paper has all the details.
The mail list can be hit-or-miss, but is often a surprisingly good resource.
Steve


Dear Laurent,
Thank you very much for your reply.
I am so lucky as Steve said. Your paper is so fresh (online on 10/9) that I did’t find it before.
I will read your new paper over carefully.
I were following your PNAS paper. Because we wanted to simulate the desalination in the future, I used gravity-induced flow instead of using pistons.
I agree with you that the friction in nanotube is very small. If we create a periodic tube without inlet and outlet and apply pressure on the water inside, the water molecules will keep speeding up? Is it the possible reason why my flow rate increases with the tube length under gravity-like pressure I am using?
Best,
Jason


Dear Laurent,
I checked Simon’s website (http://www.simongravelle.fr/). It seems that you have another paper about aquaporins that has been accepted for publication.
Could I have the link to the paper for preview? Thank you very much.
Best,
Jason



