Dear Lammps users:
I am testing pair_style coul/wolf for my polymer model. I just found out that when I used different alpha, the coulombic energy converged to different values. Below I attached two plots for alpha equals 0.2 and 0.25. The x axis is alpha times rc (cutoff distance). The plateau values of the two curves are quite different. Also, none of them is close to the e_coul+e_long calculated by ewald summation (-36676 kcal/mol). What could be the reason for this? Thanks a lot.
Shaorui
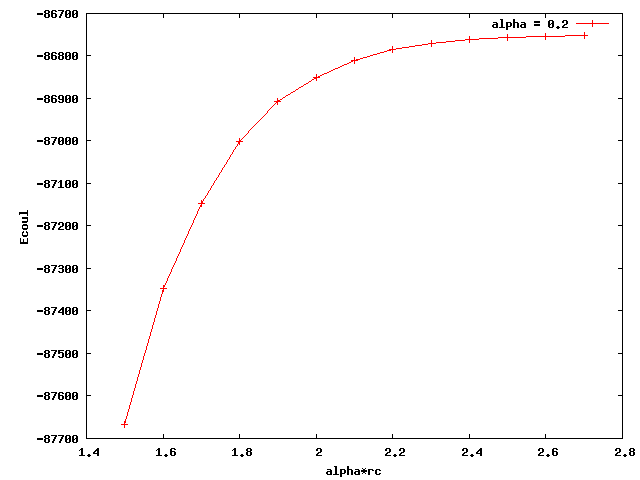
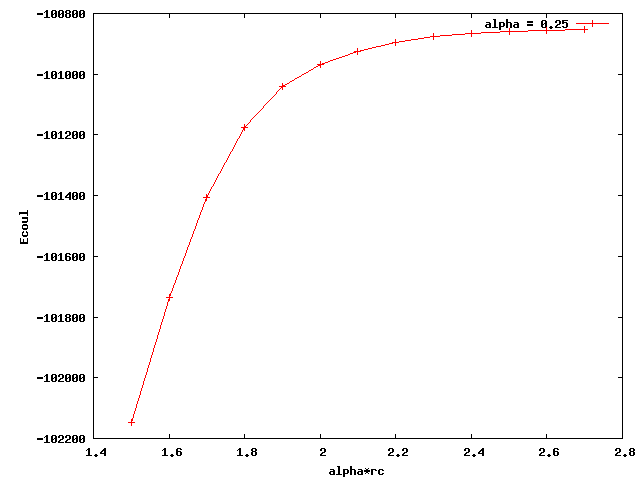
That is very normal. The “alpha” factor, in units of inverse length, controls how fast the 1/r decays. Alpha factors of 0.2 and 0.25, 5 and 4 angstroms if you use metal units, are maybe a little to short to be comparable to ewald. Experiment with smaller and smaller alpha factors and use the largest value that converges.
Also, Wolf summation is designed for periodic ionic crystals. It wouldn’t be the best idea if your polymer is not crystalline nor periodic.
Best,
Ray
Hi Ray:
Thanks for replying. I’m not quite sure whether the too large alpha (or too short inverse alpha) is a problem, since we can always pick large enough cutoff to make sure the energy converge. As long as rc*alpha approaches 3, at which erfc(x) function vanishes, the energy converges. We can use small alpha with large cutoff, as well as large alpha with small cutoff, and the energy should always converge to the same target value. I attached here another test for NaCl using alpha = .2 and .25. As expected the two curves both converges to the ewald value. Now the problem with my polymer model is that using the two different alphas (.2 and .25), both curves converge as rc goes larger, but to totally different values. That is something abnormal.
When you say wolf is not a good choice for polymer, are you talking about efficiency or accuracy? If it is just not so efficient as for crystals, I am okay with it since it is still faster than ewald\n (my box is triclinic, pppm has not option for this type of box). Thanks. Looking forward to hearing from you back.
Shaorui
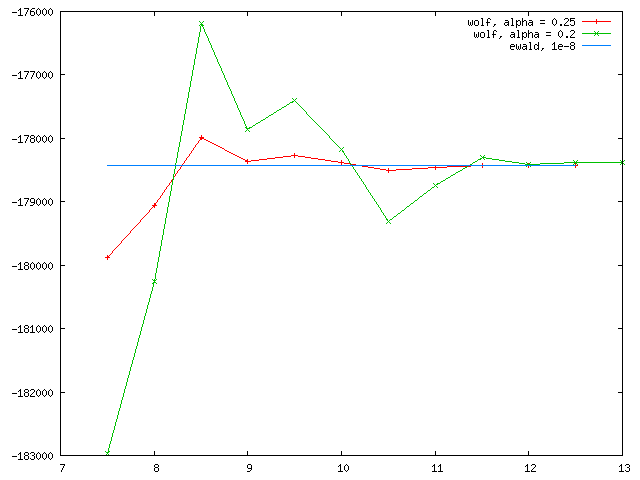
Yes, different damping should converge to the same value. In their original paper, damping for NaCl were chosen to be 0.8/a0 – 1.5/a0, which corresponds to around 0.15 – 0.25 for that particular case. For a structure with a different a0, different alpha factors should be chosen.
If the NaCl test was also performed with LAMMPS coul/wolf, then I would think Wolf sum is not the best idea for your polymer model, in terms of accuracy.
Since Wolf sum is a pairwise, spherical truncated summation that assumes charge neutral within the truncation, problems may arise if the structure is highly disordered, that is charge is not neutral within the sphere. In that case, you may need stronger damping with longer cutoffs.
Best,
Ray


