Proper computation of stress in molecular statics

LAMMPS LAMMPS Beginners
,
1

Dear LAMMPS users,

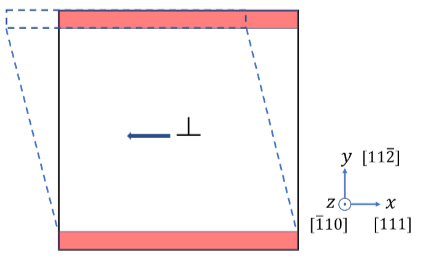
I am working on calculating the Peierls stress of an edge dislocation in an HCP crystal using molecular statics simulations in LAMMPS. My goal is to obtain the (overall) stress associated with the dislocation motion. I introduce an edge dislocation (generated using Atomsk) into a simulation box of size Lx × Ly × Lz = 100b × 100b × b, where b is the lattice constant. The boundary conditions are: periodic in the x and z directions and shrink-wrapped in the y direction. The dislocation line is aligned along the z direction, while its glide direction is along x. I limit the simulation box in the z direction to a single lattice period (1b) to prevent the distortion of the dislocation line during loading. To apply shear loading, I define upper and lower atom groups and iteratively displace the upper group in the x-direction, keeping the lower part fixed (see the image). The relevant LAMMPS script snippet is:

image_setup

label loop

displace_atoms lower move ${dx_per_step} 0.0 0.0 units box

min_style	cg
minimize	1e-14 1e-14 10000 10000

next		a

jump		SELF loop

To compute the shear stress, I sum up the xy component of the per-atom stress as follows:

compute		stress_mob mobile stress/atom NULL 
compute		stress_mob_red mobile reduce sum c_stress_mob[4]

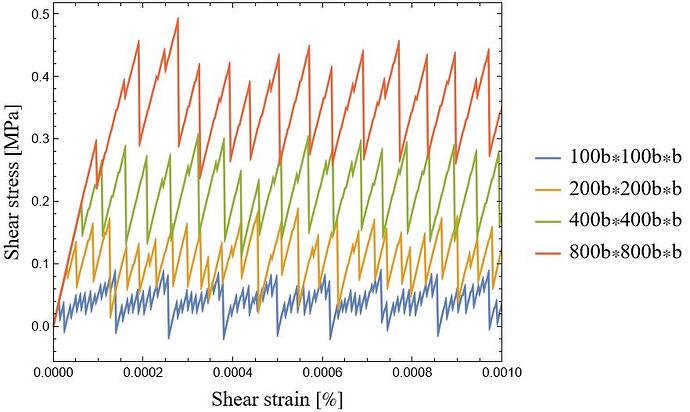
Then, I divide this quantity by the simulation volume (Lx × Ly × Lz) to obtain the shear stress. However, I see two peculiar behaviors in the shear stress-shear strain response: 1) large oscillations, and 2) as I increase the simulation box size, I expect the shear stress to eventually converge to a well-defined value. However, instead of stabilizing, the response keeps growing (see the image below). This is unexpected, as I assumed that beyond a certain system size, size effects should diminish, leading to a converged solution.

image_result
image_result882×527 65.3 KB

So, here are my question:

  1. Am I correctly calculating the shear stress?
  2. Is there a better approach for simulating this molecular statics scenario?

Any insights, suggestions, or relevant references would be greatly appreciated.

2

Have you visualized the geometries resulting from your individual minimizations? Do they correspond with your expectation of a proportional displacement of all the “in-between” atoms?
Specifically for the different box sizes?

Why don’t you just deform the entire box with the change_box command?

3

Dear @akohlmey

Thank you for your comments. Actually, I don’t observe a clear shear deformation of the system as a whole, which I believe is due to the periodicity in the x direction. As for the displacement of atoms after each minimization, I observe an atomic rearrangement after the first minimization only (which is performed at zero loading to introduce the dislocation into the system). However, I don’t see a gradual shift in the relative atomic positions as the upper rigid part is moved. There are changes happening but mostly due to the movement of the dislocation.

I have read a lot of paper on the simulation of the Pierels stress and in most cases people are using this simulation scenario. Do you think there is something wrong with my method?

Thank you again.

4

I don’t know. This is not my area of expertise. If I would want to achieve the kind of deformation you are looking for, this would be my first choice. How this reflects on the properties you want to compute, I do not know. That is something for checking the published literature, as you have apparently done already.

Furthermore, your whole topic is mostly off-topic for this forum category, since it is not really a question about LAMMPS, but about how to do your research.