Dear LAMMPS community,
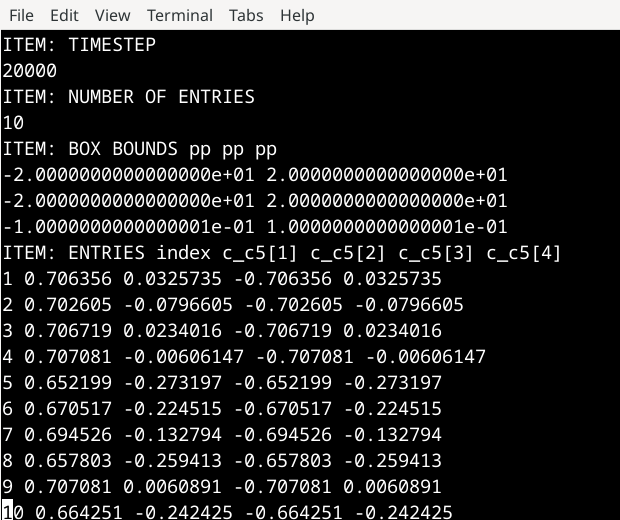
I am working on a 2d system (in XY plane) with rigid rings (composed of DPD point particles) suspended in solvent (DPD point particles). See the attached screenshot. I need to determine the rotation angle of the rigid rings about the Z-axis. To do so, I was using the “compute rigid/local”, which output the quaternions for each individual rigid ring. I noticed some discrepancy in the output (see the attachement). In particular, the quaternions for the rigid rings must be of the form (w, 0, 0, k), where w determines the rotation angle and the rotation axis must be (0, 0, k) corresponding to the Z-axis. However, for some of the rings the quaternions are not of the expected form. Further, you may notice from the screenshot that all the rings have roughly the same rotation angle but the quaternion output is otherwise. Note that, I use “dimension 2” and “fix all enforce2d” for the 2d simulations. I could not find much help on how LAMMPS calculates the initial quaternions for the rigid body. Kindly suggest any help in this regard.
The entries in the output correspond to “index of the rigid body, quatw, quati, quatj, quatk” of the compute rigid/local
LAMMPS version: Stable 29 Aug 2024 Update 3
PS: Input files attached to reproduce the reported behavior.
Thank you
in.simple (1.2 KB)

init_simple.config (286.2 KB)
Hi @sattibabu,
Please see this post where Steve explained which function to look for in the source code if you’re interested to check how quaternions initial values are computed.
As for the rest of your problem, I am unsure about the rotation referential of rigid bodies. I think it is about the initial axis set through the inertia tensor. Since they are degenerate in the case of a ring, that might explain your results. But, as I said, I am unsure about that. This should be seen in the code.
Thank you @Germain
I noticed something after your suggestion. After breaking (by assigning little extra mass to one of the particles in the ring) that degeneracy in the inertia tensor, the quaternions are coming out correct. I will look into the source code as suggested by you.
1 Like
That may not be needed. If you want to have consistent moments of inertia, you can also check out the “infile” option of fix rigid, which you can override whatever LAMMPS will compute and thus will guarantee consistent values.
1 Like
Hi - a few Qs to clarify what you asking about.
(a) (for Axel) I think we made some changes to enforcing 2d rigid bodies remain 2d, possibly in the last year. Does the code version you are running include that?
(b) Are you saying the discrepancy does not affect dynamics, but is only in the initial quat of each rigid ring?
(c) Are you saying w/out the added epsilon mass, there is a degeneracy such that all the initial quats are correct?
If (b) and (c) are “yes”, then it seems like your anaylses should not depend on the initial quat. E.g. if you are tracking the change in quats over time, then that will be independent of the (random degenerate) value of the initial quat.
@sjplimp According to git log src/fix_enforce2d.cpp the changes you are referring to were made in early April 2023, so they are definitely included in the 29 Aug 2024 stable version (they would already be in the now outdated 2 Aug 2023 stable version).
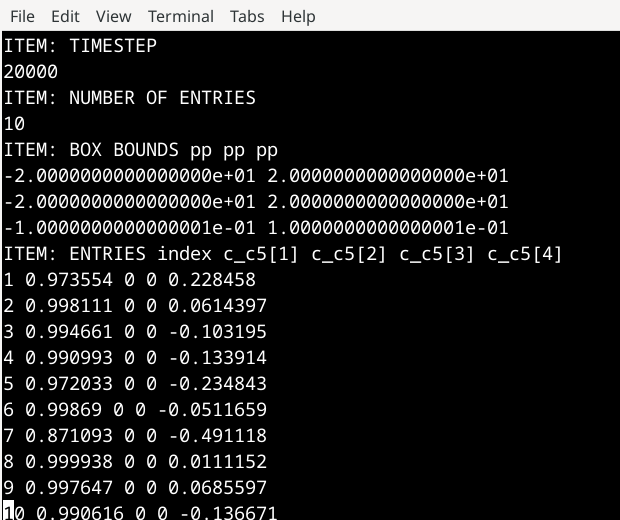
There is certainly something wrong with the 2Aug2023 version. The calculated quaternions (despite adding the little extra mass to one of the ring atoms to break the degeneracy) are incorrect. However, with the 29Aug2024_update3 version, they seem correct. (see the output from both the versions, the screenshots are named accordingly)
I believe so. There seems to be no effect on ring dynamics, but quaternion dynamics are wrong. (see the screenshots)
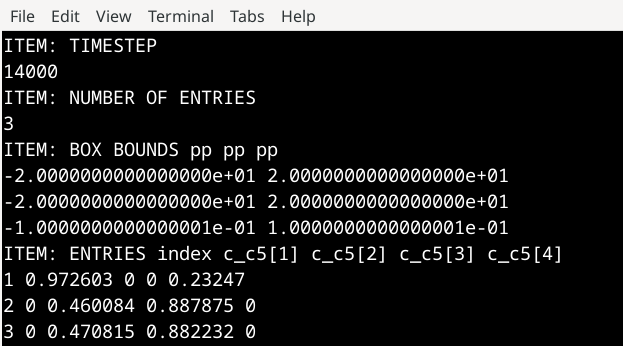
Without the added epsilon mass, there is degeneracy in the Ixx and Iyy components and the initial quaternions are wrong and continue to be so with quaternion dynamics (with the 29 Aug 2024 update3 version). However, the ring dynamics seem unaffected.
Actually, LAMMPS computes for the intertia components are identical (and correct) with or without “reinit yes” option. In that case, Is there a need for overriding what LAMMPS computes?
Where did I mention this option? I don’t recall it.
You did not specifically mention that. I was going thru the documentation (particularly the warning section about infile and reinit options for fix rigid) and referred in that context.
ok - I figured something out which I did not remember
Which is that the 3 principal axes of each rigid body (even in 2d) need to be right-handed.
The code enforces this by flipping the 3rd axis (max moment of inertia) if necessary.
In 2d, the 3rd axis is along the z-axis. But the flip means it points along (0,0,-1) instead of (0,0,1).
This means the quaternion (initially or at any time) for a 2d body can either be of the form (a,0,0,b) or (0,a,b,0). In the (a,0,0,b) case it is a rotation around (0,0,1). In the (0,a,b,0) case it is a rotation around a vector in the xy plane to flip the body upside down (180 degree rotation).
I think either of these representations are mathematically correct and thus that the dynamics in LAMMPS of the rigid bodies in your 2d simulation are also “correct”. I.e. they are responding to forces/torques from nearby bodies and solvent in the proper manner. Also, there is no need to break symmetry by adding an epsilon mass to one particle in the ring. Do you agree with that assessment?
However, I also agree that for 2d bodies it is confusing to have quats of the form (0,a,b,0).
I think we could change lines 2169-70 of fix_rigid_small.cpp to flip the x or y axis instead of z.
Then I think all 2d quats will be of the form (a,0,0,b). I need to think about this a bit more.
Steve
1 Like
This would be coherent with my small measurements on @sattibabu’s system. Two of the rings have a I_x and I_y values of 59.99 and I_z=119.99 (roughly) and the other one is I_x=I_y=60.0001 and I_z=120.00.... I suspected that these slight differences would have an effect in the enforcement of the 2d geometry such as what you mention during the initial computation of the quaternions.
I am however a bit novice in quaternion algebra so I didn’t really push the analyses further.