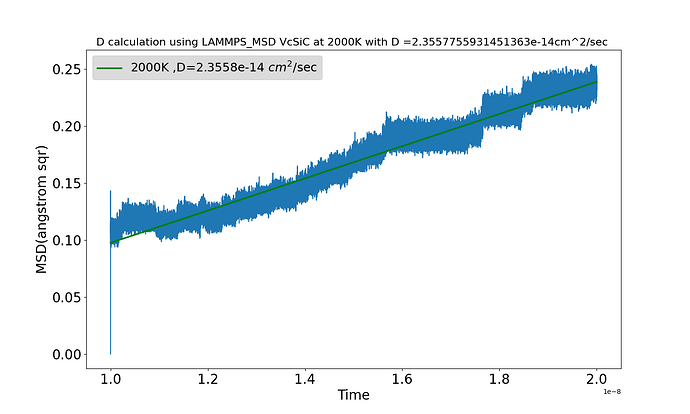
Hello everyone I am working out to evaluate MSD for calculation of D in SiC with a carbon vacancy at considerable high temperature. It’s rigid periodic system so I am not considering setting image flags.
I am surprised so see MSD decrease sometimes. while following the expression used to calculate MSD I wonder it should increase. moreover the calculated D(MSD Vs Time) is also significantly in acurate. I attached a the result and also used input
I will highly appreciate your positive response
kind regards
in.datagather2000 (1.7 KB)
If you are tracking a vacancy’s movement over time in a solid lattice, wouldn’t you expect to see overall oscillations around its occupation site, with occasional discrete jumps, sometimes backwards as well as forwards?
Hello @srtee thanks for making a comment, yes you are right overall oscillation have some contribution I can expect an over estimation but still minute, compared to diffusion event(>= 3.0 angstrom) and try to add a correction.
While you mentioned back and forth jumps, I wonder mean square displacement as sum (MSD(t) = (1/N) * Σ [r_i(t) - r_i(0)]^2) shouldn’t always increase ?
Intuitively, when calculating the MSD of n particles in d spatial dimensions as they undergo isotropic diffusion, the MSD will be decreasing (on average) 2^{-dn} of the time.
So one vacancy in three dimensions should “backtrack” for 1/8th of your observation time, which is not far off from your observations.
More importantly, the huge initial jump shows you did not have an equilibrated initial condition. Together with two separate diffusive regimes (a straight, positive-sloped line followed by “steps”) this suggests your system was undergoing a very fast relaxation (right at the start) followed by a fairly fast relaxation. You can hope it’s equilibrated afterwards, but the chances of that are fairly low and you are likely seeing a slow relaxation now at the end rather than a truly steady / equilibrated state.
But I’m just considering your system as a generic solid-state-with-vacancy simulation. Since you have spent much longer with your system than I have, of course you will be far more familiar with its behaviour than I am.
hi, srtee, i can’t understand that … as they undergo isotropic diffusion, the MSD will be decreasing (on average)
2(−dn) of the time. why MSD would decrease with time, and i suppose that MSD always increase with time based on its calculation formula. and can you share some papers about MSD decrease with time?
thank you
yes I endorse your statement I am also not convinced (basically from the MSD expression since its squared) about the decreasing MSD hypothesis. I will also highly appreciate some literature in this regard
There is a list of text books on MD in general here: Books about Molecular Dynamics generally or LAMMPS specifically
When I started out (about 30 years ago), I learned from the first one (Allen and Tildesley), which has a detailed derivation and implementation example for computing self-diffusion from both, the slope of the MSD and the integration of the velocity ACF.
I would assume the others explain this, too.
hello, akohlmey, i carefully read the content about compute msd command in the website of lammps manual. It says that
" A vector of four quantities is calculated by this compute. The first three elements of the vector are the squared dx , dy , and dz displacements, summed and averaged over atoms in the group. The fourth element is the total squared displacement (i.e., dx^2+dy^2+dz^2), summed and averaged over atoms in the group. " (second paragraph in description)
1、i wonder that whether the lammps implements the ensmble average or time average when calculating MSD with the compute msd command. With the contents copied from manual, lammps seems not to do ensmble average or time average ?
and i read some books, the definition of MSD includes ensmble average or time average.
2、if lammps just calculates the squared dx , dy , dz and total displacements, and fact is that MSD obtained by lammps can decrease with time. The reason is that the squared total displacements(refer to origin postion) at 5 ns is possibly smaller than that at 1ns.
looking forward to your reply. thank you.
What do you think it means when it says in the manual summed and averaged over atoms?
Does it say anywhere there is averaging over time?
This is not possible when the system has the diffusive (brownian motion) behavior that is assumed by the Einstein relation. Compute msd uses unwrapped positions, so if atoms leave the principal simulation cell, they will not be wrapped back by for the MSD calculation.
hi, you can have a look my latest discussion with akohlmey, hoping it can be helpful for you.
Most textbooks do not deal in-depth with small systems, because:
- Small system simulations do not (directly) give valid results for bulk systems
- Small system results are easily obtained through foundational probability or direct simulation.
This is one of those results.
First consider a 1D stepper that randomly walks either backwards or forwards. Half the time it will take its next step towards the origin rather than away, so during that step its square displacement will be reduced.
Now consider two such steppers, uncorrelated. A quarter of the time, both steppers will simultaneously step towards their respective origins. Generalising, n steppers will all step towards the origin 2^{-n} of the time.
Now consider a 3D stepper. In a simple isotropic space its x, y and z motions are uncorrelated. So you might as well consider it as 3 uncorrelated 1D steppers instead of 1 3D stepper. By simple logic, n uncorrelated steppers in 3D space will all be stepping back towards the origin all at once 2^{-3n} of the time.
Of course this is irrelevant for almost all MD simulations. If you simulate 10 argon atoms in 3D, all of them will step towards the origin in x, y and z simultaneously about 2^{-30} of the time. As a quick hack, 2^{10} \approx 10^{3}, so this is about a billionth of the time – or, if you simulate in 1 fs timesteps, you will have to simulate the system for about 1 microsecond to see one femtosecond-timestep in which all argon atoms are simultaneously moving towards the origin instead of at least one moving away.
But if you are simulating a single vacancy then MSD can most certainly decrease over time for statistically detectable portions of your trajectory.
1、summed and averaged over atoms
MSD(t) = (1/N) * Σ [r_i(t) - r_i(0)]^2 (taken from Irslan_Ullah_Ashraf’s reply). I reckon that summed is Σ, sum the MSD of all atoms in specified group; averaged is 1/N.
2、ensemble average or time average
what i want to say is that assume MSD(t) = (1/N) * Σ [r_i(t) - r_i(0)]^2 = R(t) - R(0), and there might be MSD(t) = R(2t) - R(t), MSD(t) = R(3t) - R(2t),…, so eventually the MSD(t) should be the average of all MSD(t).
3、
3.1 suppose that i calculate the MSD of a silica nanoparticle surrounded by other base fluid, is there any possible that nanopartilce return to its origin position at 5ns or any other time, if this happen, then the MSD would be much small ? (actually I obtained the MSD of nanoparticle sometime decrease with time)
3.2 Compute msd uses unwrapped positions—— I calculate the MSD by compute MSD command in lammps using rerun, and the coordinates in dump file is wrapped, do i need to ensure the unwrapped coordinates in dump file for rerun to obtain a accurate MSD ?
Thank you in advance for your reply
Yes. If the image flag information is not there your MSD results from rerun will be completely bogus.
This is impossible since compute msd only stores one origin. You must not assume something that is not mentioned in the documentation.
akohlmey, thanks a million.
1、would you help me check that whether the dump command in my input scripts hold the image flag information
“boundary p p p
dump 1 all custom 10000 dump_MSD_3ns.lammpstrj id type q mol mass x y z vx vy vz fx fy fz”
i guess the above dump command couln’t store the the image flag information, is this right ?
2、I rewrite it
dump 1 all custom 10000 dump_MSD_3ns.lammpstrj id type q mol mass xu yu zu vx vy vz fx fy fz ix iy iz
the dump file produced by this dump command can give me a accurate msd result with rerun ?
thank you again!
Thanks for referring it’s really insightful and guiding. stay blessed
I am not an input file approval service. To figure out whether what you are doing has meaning is your job.
All the information you need is in the LAMMPS manual. Please re-read the compute msd documentation (again) and pay special attention to the “Note” sections.
Please note that you can very easily confirm the correctness of your rerun input by comparing it to the results you would get during the regular MD run. Just set this up with a small system and short test run. You don’t need to look for converged results, you just need to confirm that both give the same intermediate values within floating point rounding accuracy at every recorded MD step.
oh, i see, thank you. I won’t bother you with this sort of problem. I am also checking it with running another simulation.
thank you again.