Questions about compute omega

LAMMPS LAMMPS Beginners
1

Dear LAMMPS Developers:
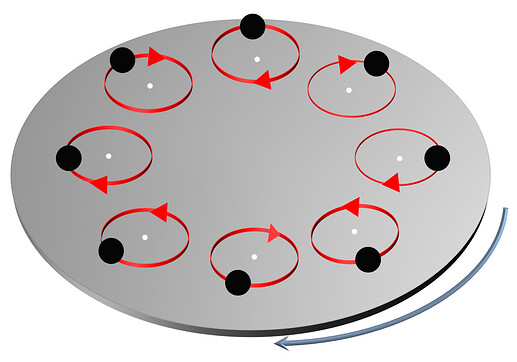
We would like to calculate the angular velocity associated with the overall rotation of the lattice. However, we have some uncertainties regarding the physical interpretation of the angular velocity, denoted as omega, in LAMMPS. In our specific setup, the atoms of the lattice simultaneously undergo two types of rotation: a local rotation around their individual equilibrium positions and an overall rotation about the centroid of the system. As shown in the disc sample below , black dots represent the atoms, white dots represent the equilibrium position of the atoms, the red circle represents the local rotation, and the blue arrows represent the overall rotation of the lattice. In this case, the mechanical angular momentum calculated by the LAMMPS compute command, that is, the total angular momentum of all atoms with respect to the centroid of the lattice, denoted Lz, contains contributions from both local and overall rotations.

We are seeking clarification on whether the angular velocity obtained from the commands ‘compute omega’ and ‘compute omega/chunk’ in LAMMPS corresponds to the angular velocity of the overall rotation of the lattice as described in our system. Alternatively, does this angular velocity result from the formula w=Lz/Iz, where Iz is the moment of inertia relative to the center of mass. Obviously, w does not correspond to the overall rotation of the lattice, since the latter is equal to the corresponding angular momentum of the overall rotation rather than the total angular momentum Lz, divided by the inertia moment.

We would like to get the physical meaning of omega, for our particular system, whether it also represents the overall rotation velocity of the lattice.

We would appreciate any guidance or assistance regarding this matter. Thank you very much for your attention.

1472c75532e09868dcc67d9f7562811
1472c75532e09868dcc67d9f75628111323×927 124 KB

2

There is no ‘compute omega’ command in LAMMPS.

What is computed by ‘compute omega/chunk’ is described in the documentation for that command.

Interpretation of the data is not the job of the LAMMPS developers, but that of the user. If you feel insecure, you should apply the scientific method to get insight (i.e. formulate a hypothesis, set up some simple tests that would either confirm or conflict with the hypothesis, observe the results and either repeat with a modified hypothesis or stop).

3

Thank you for your prompt reply!

  1. I apologize for the clerical error in my previous message; I intended to refer to the “variable omega() function” command.
  2. I understand that LAMMPS provides two commands for calculating angular velocity: the variable omega() command and the compute omega/chunk command. However, I would like to clarify whether the angular velocity computed by LAMMPS accurately represents the true angular velocity of the overall rotation of a non-rigid system. Specifically, I am curious whether the developers of LAMMPS took into account that the angular velocity calculated as Lz/Iz may not reflect the overall rotation of the non-rigid body, given that this value also incorporates contributions from the atoms that vibrate or rotate about their equilibrium positions.
  3. Thank you for your suggestion; however, we are unable to test this issue directly, as there is no method available for measuring the angular velocity of the overall rotation of a non-rigid body. Consequently, this limits our ability to compare experimental results with the calculations generated by LAMMPS.

I came across a similar question posted in the community in 2022, but unfortunately, it was not addressed with sufficient clarity. [Feature Proposal] Fix momentum angular for non-rigid groups of atoms - LAMMPS / LAMMPS Development - Materials Science Community Discourse (matsci.org). As a result, I am uncertain whether the current version of LAMMPS effectively resolves this issue.

Looking forward to your reply! Thank you very much!

4

As I already wrote, LAMMPS computes what the documentation says it does. Nothing more, nothing less. And if you don’t trust what the documentation says, you have to read the source code. That is the way it is and always has been.

When you are using a term like “true angular velocity” you have to explain what you mean by that and how that would differ from what is computed by LAMMPS. The burden of proof of whether there is a difference lies on you and not on the LAMMPS developers. After all, you did not contract the LAMMPS developers to develop features specifically for you and exactly the way you intend them to be.

To the best of my knowledge, those computations look at instantaneous values and thus do not at all care whether atoms are part of a rigid body or not. Corresponding properties of rigid bodies are computed and stored separately within the rigid fix class and can be accessed with compute rigid/local.

Again, the burden of proof is on you and particularly how you would separate what you call the “true” rotation from vibrations and deformations etc.

It seems that you have not fully understood how the scientific method works.

You very well can make tests like I have suggested. I would set up simulations, e.g. with just two atoms in 2d where you can very well control whether you have vibrations and rotations and can with paper and pencil estimate what a simulation should have, assuming a simulation with fix nve and setting proper initial velocities to the atoms. Then you can generate different scenarios, formulate what your expected results should be and observe whether LAMMPS can reproduce them. You can then in small steps make things more complex and follow how the computed results are aligned with your expectations. And so on and so forth.

That is what you claim, but have failed to provide proof for.

It is not at all clear at the moment, whether there is a real issue or whether the problem is just an incorrect interpretation.

5

Please note that, since LAMMPS is open source, a little bit of knowledge enables you to check the source code and thus verify for yourself what a particular LAMMPS function does.

In this case, some inspection (I am just scrolling GitHub on my phone) shows that omega is calculated in variable.cpp via the group->omega function (lammps/src/variable.cpp at f00addcfaf4351b15de25b35e41378d24b5361f7 · lammps/lammps · GitHub), with invocations of group->angmom and group->inertia along the way.

The group->omega function in turn calculates omega using the relation L = I \omega (lammps/src/group.cpp at f00addcfaf4351b15de25b35e41378d24b5361f7 · lammps/lammps · GitHub), for which L is the usual angular momentum calculated using group->angmom (lammps/src/group.cpp at f00addcfaf4351b15de25b35e41378d24b5361f7 · lammps/lammps · GitHub) and I is the usual moment of inertia calculated using group->inertia (lammps/src/group.cpp at f00addcfaf4351b15de25b35e41378d24b5361f7 · lammps/lammps · GitHub).

Finally, the inversion operation uses a function in MathExtra called angmom_to_omega (lammps/src/math_extra.cpp at f00addcfaf4351b15de25b35e41378d24b5361f7 · lammps/lammps · GitHub). Based on the comments this function takes both the eigenvalues (principal axes’ moments of inertia) and the permutation columns (rotation into the principal frame) and calculates the box frame \omega by permuting L into body frame, dividing by eigenvalues, and permuting the resulting \omega back into box frame.

From this description hopefully it is clear exactly what variable ... omega calculates. This is a standard solid mechanics calculation of the angular velocity of an extended object.

1 Like
6

As @srtee has explained. LAMMPS computes the angular velocity by following the inversion of L = I\omega.

The feature proposal that I posted some years ago ([Feature Proposal] Fix momentum angular for non-rigid groups of atoms) refers to implementing a computation of \omega that follows the procedure described in section II.A doi.org/10.1063/1.474493. The crux of the issue is that when you consider a group of atoms that are not a solid body (e.g. a molecule that can vibrate) then what is usually considered \omega = I^{-1}L will have some component from the vibrational motion of the constituent atoms. So in this context what is considered the “true” \omega is not exactly the same as a rigid body.

As @akohlmey has said, it’s up to you to define what \omega means in your system and you can definitely perform tests to compute \omega through different procedures (you only need positions and velocities, nothing fancy).

I have some more references on how to separate vibrational and rotational motion in molecules (again, the loose definition of molecule here just means a group of atoms that are bonded in some way, so the definition could apply to your system, I think). If that is a method that you want to pursue then I will be happy to help.

7

It’s useful to be clear about the physical concepts below, even if we have to introduce some terminology to get there:

LAMMPS’s variable ... omega is coded to calculate a group’s “rotational” angular velocity, where “rotational” denotes that the angular motion is taken around the group’s center of mass (CoM). omega does not depend on a group’s linear velocity; neither does the group’s “rotational” angular momentum, and I include the proof for both below.

omega can be meaningfully “adjusted” for the group’s “orbital” angular velocity – taken around some meaningful box-frame center. For concreteness, consider the Earth in the Solar System – it rotates about its CoM every 24 hours, and orbits about the Sun every 365(.25…) days. Because the Earth orbits the Sun, its “rotational period” meaningfully differs on the choice of frame: the mean solar day, “adjusted” for the Earth’s orbital motion, is about four minutes shorter than the sidereal day (taken in “box” rather than “orbital” frame).

However, with periodic boundary conditions, the positions of both a group’s CoM and its constitutent particles are (countably infinitely) multiple-valued, and since the angular momentum is position crossed with momentum, it also is multiple-valued. There are ways to work with this (“itinerant displacements” in the electrostatics literature), but they would certainly be very complicated and of doubtful physical validity. But if you can’t even define a unique orbital velocity, you certainly can’t adjust the rotational velocity for it!

The situation is very different for the angular velocity of parts of a group relative to the group’s CoM – maybe call it the “atom-in-molecule” dynamics or velocities. In that situation one can choose different frames for the group that meaningfully describe group parts’ motions in physically relevant ways (for example, charges’ changing movements relative to CoM constitute the dielectric response, and different frames will give different numerical results).

==========

Proof that L and omega are invariant in linear velocity

Consider N particles each with mass, position, and velocity m_i, \mathbf{r}_i and \mathbf{v}_i respectively. We measure positions in the CoM frame, and thus \sum_i m_i \mathbf{r}_i = \mathbf{0}.

We define the usual angular momentum:

\begin{align*} \mathbf{L} &\equiv \sum_i m_i \mathbf{r}_i \times \mathbf{v}_i \\ &\equiv \sum_i [ m_i \mathbf{r}_i \times (\mathbf{u} + \mathbf{u}_i)] \\ &= \left(\sum_i m_i\mathbf{r}_i\right) \times \mathbf{u} + \sum_i m_i \mathbf{r}_i \times \mathbf{u}_i \\ & \overset{!}{=} \sum_i m_i \mathbf{r}_i \times \mathbf{u}_i \end{align*}

where the only assumption we make on \mathbf{u} is that we set the same “offset velocity” for all N particles. Following standard manipulations using linearity and the observation that the zero vector crossed with anything gives the zero vector, this shows that the same angular momentum will be measured about the CoM no matter what linear velocity we assign to “the group” vs “individual particles”. Since \mathbf{\omega} is a linear transform from \mathbf{L}, it too does not change.

8

I apologize for responding so late. Thank you so much for your help! Your answer was really useful—I checked out the source code and finally understood how LAMMPS developers calculate angular velocity, angular momentum, and rotational inertia. I also compared these with the same quantities from my own research, and it was pretty interesting! Your guidance pointed me in the right direction!

9

Sorry for the late reply. It’s been a pleasure discussing this with you! As you mentioned, in a non-rigid body system, the omega calculated by LAMMPS includes contributions from atomic vibrations and local rotations, which makes defining the overall rotational angular velocity of the system a bit tricky.

Lately, I’ve been thinking about how to separate vibrational and rotational motion, so if you could recommend any relevant references on this topic, I’d really appreciate it!

10

Thank you so much for your detailed reply—it’s clear that you have a deep understanding of the topic. I’ll need some time to digest everything, but I’ll get back to you with a more detailed response once I’ve had a chance to process it all.

Thanks again for taking the time to address this issue. Your support has been a huge encouragement for my research and my journey with LAMMPS!