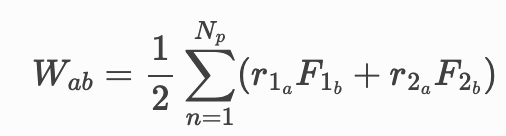I’m running a simulation where I want to calculate the virial shear stress between particles that only interact via repulsive contact forces. The issue is that when I calculate the shear stress due to this interaction by hand it differs from what LAMMPS outputs.
The LAMMPS documentation is pretty clear how the virial shear stress is calculated in this situation (the screen shot shows the only terms involved):
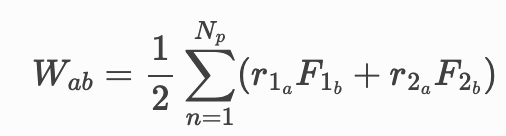
Here the r’s are the positions and the F’s are the forces of the two particles involve in a contact. The sum is over all contacts, but in the simple example I’m testing there’s only one contact.
I guess my questions are 1) are there any know bugs regarding the shear stress calculation in LAMMPS and 2) any ideas for why my calculation might differ from LAMMPS if there isn’t a bug?
Note: when I say “calculate by hand” I mean that for a given time step I print out the forces and positions of particles as well as the individual shear stresses that LAMMPS calculates. Then using the r’s and f’s I plug into the above formula and get an answer that is ~ 1.98 times as big as LAMMPS. What’s so confounding is the above formula is really simple and I’m getting a different answer. And if I was really just dropping a factor of 2 the ratio should be closer to 2 than 1.98.
It would be best, if you provided the exact input that you are using and explain what exactly you are computing how and to what you are comparing it.
The shear stresses I’m comparing to are calculated by this line in the input file:
compute indivsxy all stress/atom NULL virial
which is then dumped to a file later as “c_indivsxy[4]” which gives the xy virial shear stress calculated above.
During the run I print out the positions, forces, and individual shear stresses for each disk at every time step. For the example I’m considering (two disks numbered 140 and 1341 touching only each other) I get
x_140 = -6.392493
x_1341 = -5.442501
F_y = 0.00096074
Plugging into the expression given by the documentation above I calculate
W_xy = (1/2) ( x_140 * F_y + x_1341 * (-F_y ) )
= -0.000456
However, the compute command above gives
W_xy = -0.000231
And the ratio of these is about 1.98 (if you use all the digits …).
This is still missing the input deck.
Do you mean the input file? I’ve copied that below (wasn’t allowed to upload it).
Input file:
#2D shearing of frictional particles in suspension
units lj #EVERY THING IN SIMULATION UNITS
dimension 2
atom_style sphere
boundary p p p
newton off
comm_modify vel yes
box tilt large
read_data ${ic_file}
#read_restart ${restart_dir}/s${init_strain}.restart
pair_style gran/hooke/history 2.0 2.0 3.0 NULL 1.0 1
pair_coeff * *
timestep 0.002
neighbor 1 nsq #0.0.04.20951nm is skin = 1 Angstrom
neigh_modify delay 10 #Every 10 steps
comm_modify vel yes
#UNIFORM SHEARING
variable L equal ly
variable totsteps equal ceil(${strain}/(${gammadot}*0.002)) #SHEAR FOR TOTAL STRAIN INPUTTED
variable dumpsteps equal ceil(${dgamma}/(${gammadot}*0.002)) #DUMP IT OUT EVERY 0.1% STRAIN
variable avgdatasteps equal ceil(${dumpsteps}/1000) #AVERAGE STRESS AND THERMO OUT EVERY % STRAIN
variable shstr equal xy/ly
variable rounded_shstr format shstr %08.4f
variable strain1 equal ${init_strain}
variable strain2 equal ${init_strain}+${strain}
variable fmt_strain1 format strain1 %08.4f
variable fmt_strain2 format strain2 %08.4f
compute myTemp all temp/deform
compute myPress all pressure myTemp
compute myVirial all pressure myTemp virial
compute forces all pair/local fx fy p1 p2
compute ids all property/local patom1 patom2 ptype1 ptype2 # ids and types of atoms within a contact force
compute indivsxy all stress/atom NULL virial
variable sxy equal -c_myPress[4]
variable vxy equal c_myVirial[4]
fix 1 all nve/sphere
fix 3 all deform 1 xy erate ${gammadot} remap v flip no
fix lan all langevin 0.0 0.0 10.0 48279 omega yes
fix_modify lan temp myTemp
variable tim equal time
run 0
thermo_style custom step v_shstr fnorm ke etotal press pxy xy v_tim v_sxy v_vxy c_myTemp
thermo ${dumpsteps}
fix 4 all enforce2d
thermo_modify flush yes format float %2.15g
#dump_modify write_positions format line "%d %.6lf %.6lf %d"
dump write_forces all local ${dumpsteps} forces_s${fmt_strain1}-${fmt_strain2} index c_ids[*] c_forces[*]
dump write_positions all custom ${dumpsteps} positions_s${fmt_strain1}-${fmt_strain2} id x y type
dump write_stresses all custom ${dumpsteps} indiv_stresses id c_indivsxy[4] # sxy for each atom
dump_modify write_positions format line "%d %.6lf %.6lf %d"
run ${totsteps} every ${dumpsteps} "write_restart ${restart_dir}/s${rounded_shstr}.restart ```
What is the volume of the system?
I’m pretty sure in the stress/atom compute the value you get back is stress*volume whereas the pressure compute is already divided by the total volume of system, so without a volume correction the values won’t match
“Input deck” means everything required to reproduce what you ask about. Ideally, that is just the input file, but in your case, it also requires the data file you use and - due to excessive use of variables - the command line or a log file from a run, so that one can see which values are used.
Variables can be a great thing, but they can also make debugging and reproducing of run extremely tedious…
I think you might be right that lammps gives stress * volume (or area in this case) for the total shear stress. But for these individual particle shear shear stresses I’m not sure; I’m only off by a factor of ~1.98 and the area of the system is ~2500.
So there are four files in my input deck. Theoretically you should be able to download them all to the same directory on a linux system and do “python run.py” and get the same output as me.
Because I’m a new user I couldn’t upload them here but here’s a link to my personal website where I’ve posted them: http://willbuchholtz.com/pages/Documents.html
Ok, so here is where I think your problem lies:
The formula that you have quoted to compute the accumulated per-atom stress is looping over the forces for all pairs of atoms, that is for each iteration of the two nested loops of over the neighbor list (first over all “local” atoms, then over all neighbors of those atoms). These forces are obviously different from the accumulated per-atom forces that you print out in a dump file. There is an additional twist in that, because the atom positions for atoms from neighboring subdomains (aka ghost atoms) are those positions, but in the dump file you only have the local positions.
In short you are comparing apples and oranges and the difference factor is just a coincidence.
I think you’re right that I’m comparing apples and oranges. But I’m still confused.
When I print out the forces I’m using the compute pair/local command (in combination with compute property/local) which according to the documentation gives properties of “individual pairwise interactions.” I think I’m printing out individual contact forces; I don’t see how these are the accumulated forces on each atom (which I’m assuming means the “net” force).
Big picture though, I just need to be able to print out all the contact forces and particle positions in the system at a given time step. Do you know how I can do this correctly?
There is not much of a point to continue discussing this without you having studied the source code.
Please also note that the expression you are looking at applies in this general form only to point particles and simple, pairwise additive potentials. Since you are using extended particles and a granular pair style, the actual stress accumulation is a bit more complex.
You should see the stress accumulation from any calls to ev_tally*() or v_tally*() functions in the compute() method. Those tally functions are defined in the Pair base class.
When using compute pair/local, you are using a different code path that executes the single() method of the pair style. How well that corresponds to what compute() computes depends on the individual pair style. Please note that the resulting force is the total force between the two particles that will need to be projected on delta_x/r, delta_y/r, and delta_z/r to get the force components in x-, y, and z-direction.
Ok. This is helpful. And yeah I guess I need to study the source code.
Ultimately it may be easier/safer to just have lammps calculate the shear stress on each particle for me. (I may have to go back and regenerate some data but whatever.) But now I’m nervous to use the stress/atom command for that because I have extended particles with a granular pair style.
Can I use stress/atom to get the shear stresses or do I need a different command? Sorry if this is a dumb question but based on the documentation I would have thought I could.
Compute stress/atom does what it’s documentation says it does. As was commented earlier, it computes a local stress*volume property and you need to divide it by the appropriate volume to get the stress. Determining that volume on a per particle level is often not easy. The volume is only well defined for the entire system. Please see how stress/atom is related to the total pressure tensor of the whole system in the documentation.