Simulating surfaces (slab method) — Questions with regard to solvers and possible atom loss

[Amr_Ramadan]

Hello everyone,

first off let me preface this query with the fact that I have experience with different atomistic simulation packages, but only just recently started to learn to use the LAMMPS package.
The version I am using is the stable version (9 Dec 2014), which I run on a linux based cluster of our university (should any further details be required with regard to the system specifications let me know). Most test calculations have been performed on a single core for small systems.

I am interested in simulating free surfaces for SrTiO3 using pair potentials, to this end I have been successful in simulating 3D periodic bulk SrTiO3 with the potential of choice using the Ewald long-range solver for the Coulombic interactions and a Morse potential for the short-range interactions. I use the HFTN minimizer as it yields the lowest resulting cell pressure (in comparison to the cg solver). I assume this is simply a result of how the solvers calculate the pressure.

Due to personal preference I use the fixedpoint 0.0 0.0 0.0 command in the box/relax fix. Once I have optimized the bulk structure, I replicate the cell to the desired size (for the test caluclations I use “replicate 4 4 4” which is a cell with 320 atoms). As I use the Ewald summation for the Coulomb interactions, I implement the “kspace_modify slab 3.0” option and change the boundary condition to “boundary p p f” and accept that I am restrained to orthogonal boxes as SrTiO3 has a cubic structure. Is there any information with regards to when triclinic boxes within the slab method will be implemented in the LAMMPS code?

The problem I encounter is that in some cases after the optimization is completed I get this error message:
“ERROR: Atom count is inconsistent, cannot write data file (…/write_data.cpp:149)”

I then reran the simulation with the added command “thermo_modify lost ignore” and view the resulting structure from the dump file and find that the optimized structure appears reasonable however a few atoms were relaxed to a position outside of the z-bounds of the box. If I understand the slab option correctly, then it implements a vacuum in the non-periodic dimension which is reproduced periodically due to how the slab method works. Hence, the loss of atoms confuses me. Especially since the error is not always present/consistent, as it most likely depends on the initial configuration (whether the atoms are located very close to the box bounds or not).
In one case the error appears if I refresh the neighbor list frequently (neigh_modify every 1 delay 0) and does not appear if I leave the neighbor settings at their default values. However, I have not found a way to reproduce the error in a consistent way.
Is there away to ensure that the error does not occur? Is it safe to assume that if the error does not appear that the simulation was successful?

I also tried to us the box/relax fix combined with the slab option to relax the periodic directions (x and y) with the following command:
“fix box_relax all box/relax x 0.0 y 0.0 couple xy vmax 0.10 nreset 1 fixedpoint 0.0 0.0 0.0”
Although the simulation completes, it does not change anything not even the atom positions as with the run without the box/relax fix. I do not know what is happening here, any help/explanations would be appreciated.

While reading the documentation of the slab command I came across the possibility of implementing a wall fix in order to prevent particle migration beyond the initial z-bounds. From my limited understanding of wall fixes, I believe a rough wall could fulfill the requirement of not losing atoms, but I am unsure whether it will allow the relaxation of these atoms as a free surface. Any additional information on this matter would be of great help to me.

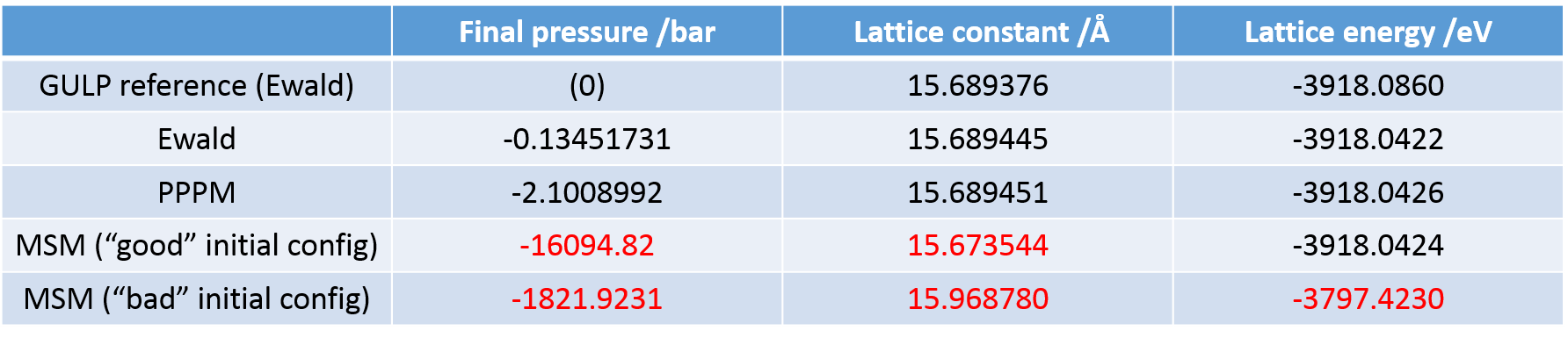
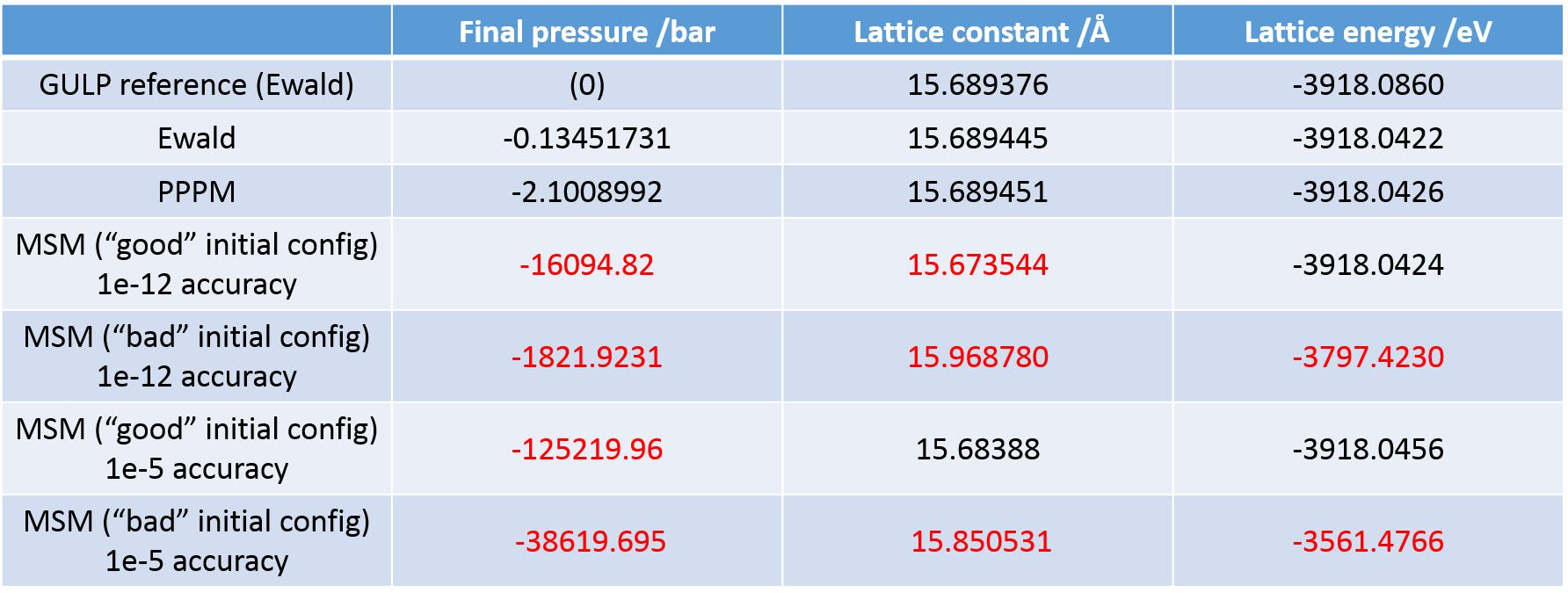
On a different note, I tried to implement the MSM solver for the long-range interactions for the same system as it allows non-periodicity in all three dimensions for triclinic systems, and encountered some difficulties in obtaining the same energy and box size I would get using the Ewald solver for the periodic bulk cell with the same initial data input. Furthermore, the final values given by the solver differ significantly depending on the initial configuration I input for the calculation (in this case I isotropically varied the initial box size). This inconsistency would prohibit the use of the MSM solver for the investigations I intend to perform. I use an accuracy factor—although it appears to be computationally expensive—of 1E-12 (“kspace_style msm 1.0e-12.0”). Is there any known reason for such discrepancies?
Even when I use a starting configuration close to the minimum, I do not obtain the value I would expect from using the standard Ewald summation.

Finally I had a question with regards to visualizing the slab simulations in Ovito (v2.4.2). As I understood it from the manual the “kspace_style slab 3.0” command internally inserts a vacuum in the simulation cell in order to obtain the free surface, however when I load the dump file into Ovito and show “periodic” images the inserted vacuum is not present (as it is not included in the dump file). Is it possible to dump the slab geometry with the vacuum portions in such a manner that it can be visualized with typical viewing programs?

For example input files see attachments:
*.lat is the input lattice via read_data.
*.in is the input script as was used in my test calculations
sto_bulk.lat was also used with sto_bulk_msm.in.

So to summarize my questions:

1. Is there any news on when triclinic box support will be implemented for the “kspace_modify slab 3.0” option?

2. Is it possible to reduce the possibility of atom loss due to the initial positions being close to the cell edge? Is it safe to assume that if the error does not appear that the simulation was successful?

3. Can an implementation of the wall fix be helpful in this case, and will it be equivalent to minimizing a free surface? If so, what kind of wall fix would be ideal?

4. The anisotropic box/relax fix does not seem to work with the slab option.

5. What is the reason for the different results obtained when using the MSM solver? Can it be corrected/fixed?

6. How can one best visualize the slab configuration when simulating surfaces?

Thank you in advance for your help. Should there be any required information missing, I will be happy to supply it.

Sincerely,
Amr Ramadan

sto_bulk_msm.in (1021 Bytes)

sto_surf.in (1023 Bytes)

sto_surf.lat (55.7 KB)

sto_bulk.in (984 Bytes)

sto_bulk.lat (1.16 KB)

[Stan_Moore]

For point 1, there is some question on whether the slab approximation is valid for triclinic systems, so it hasn’t yet been implemented. I’d have to think about it more.

For point 5, you say that you do not obtain the value expected from using the standard Ewald summation when using MSM. Different methods give slightly different forces, which could alter the path of minimization to find a different local minima, so it is hard to know if something is wrong here. Have you tried using PPPM, and is that different too? For MSM, are you using boundary p p f, or boundary f f f? I’ve found MSM to work great for all nonperiodic systems, but for slab systems, MSM convergence is slower than expected.

Stan

[Amr_Ramadan]

Dear Stan,

thank you for your reply! With regards to point 5:

In the case of comparing the different methods, I used fully periodic conditions (“boundary p p p”) in order to keep the initial test simple, hence I would expect the same result (with maybe minor differences in final energies/pressures/lattice constants). The non-periodic simulations were only tested using the Ewald method and the kspace_modify slab command.
I had not tested the PPPM method yet, but it seems to run much slower compared to the Ewald method when using the same accuracy (1E-12), contrary to what the manual states. However the results when I reduced the accuracy to 1E-8) are in good agreement with what the simulations with the Ewald method yielded. Only the MSM method does not converge within the same error range as the other methods, be it with a good initial configuration, or a bad initial configuration with multiple subsequent minimizations.
I attached an image summarizing the results and comparing them to the results I obtained for the same system and potential using the GULP code, which employs the Ewald method as well.

The deviations observed between the GULP reference, Ewald and PPPM methods are all within the margin of error and acceptable in my opinion. However, the difference I see with the MSM method is almost OK when using a good initial configuration (I find the change in the lattice constant to be too large) but definitely too far off when using a bad initial configuration. I do not believe that this is simply the result of slightly different forces. This is important because I might not always know whether I have a good initial configuration (even if I intend to try to always start with one).

With regards to the final pressure, this seems to be the most inconsistent factor as I have seen it vary depending on the minimizing algorithm I use (eg. hftn or cg). Best results for me were obtained with hftn. But in the test calculations shown here, only the hftn minimizer was used.

Amr

[Stan_Moore]

Your 1e-12 accuracy tolerance is extremely small. This will work fine for Ewald if your system size isn’t too large, but as you observed it causes PPPM to be slower than Ewald. A typical value is 1e-4 to 1e-5. For MSM, the method tries to automatically adjust the real space cutoff to speed up the simulation, but for a tolerance of 1e-12, it is most likely using a very large real space cutoff with very little computation in kspace. For MSM, you could try using 1e-5 instead and see if you get more reasonable results. You could also trying using “kspace_modify cutoff/adjust no” with MSM, but your simulation will run much slower unless you use an accuracy tolerance more like 1e-5 instead of 1e-12.

Stan

[Amr_Ramadan1]

Dear Stan,

thank you for your quick reply. I would like to apologize for my late reply as I was out of office (vacation) for 3.5 weeks.

I tested the MSM calculations as you suggested with a lower accuracy tolerance (1e-5). Below is the updated table

Correct me if I am wrong, but the MSM solver appears to have a tendency to get stuck in local minima within the energy landscape and is very dependent on the initial input configuration, making it all the more important to have good starting positions. As far as I can tell MSM does not appear to be ideal when it comes to optimizing the pressure of the system.
If however this is not usual for the MSM solver, I will be more than happy to send a short example input script if it will help to find out what the problem is.

Thanks again for your help so far.

With regards to the other questions I had in my initial post, I think it would be better If I try to ask about them in a separate mail, where the questions could be phrased shorter and more to the point.

Best wishes,
Amr

[Stan_Moore]

If you use Ewald or PPPM with a larger error tolerance (1e-5) do you get similar results for pressure as with MSM? MSM is best for low accuracy. You could try using “kspace_modify cutoff/adjust no pressure/scalar no” with MSM, but you aren’t going to get it to agree for several decimal places without a lot of cost. With crystals being so incompressible, a little error in positions can lead to a huge pressure difference, so it is hard to tell if this is a bug.