Dear all
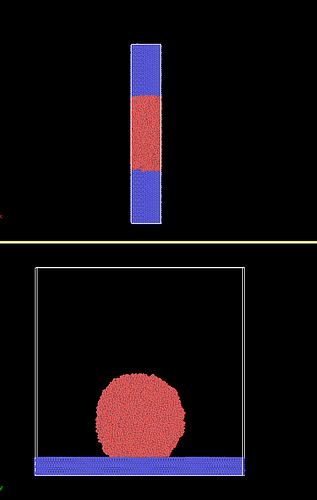
I used the mW potential function to calculate the contact Angle of a cylindrical droplet, with a radius of 50 angms and a height of 40 angms, and I put 10000 atoms, and the configuration diagram is shown here
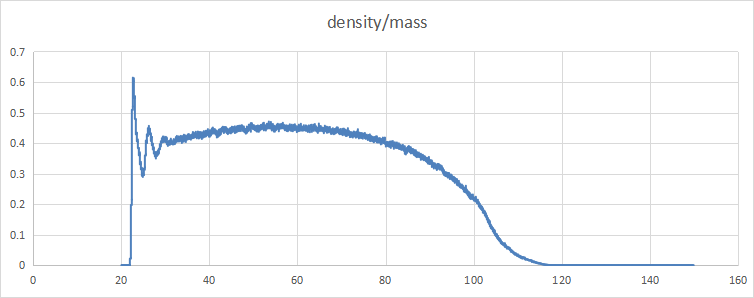
Density /mass and density/number are calculated by using the statistics command provided with LAMMPS as shown in the figure below.
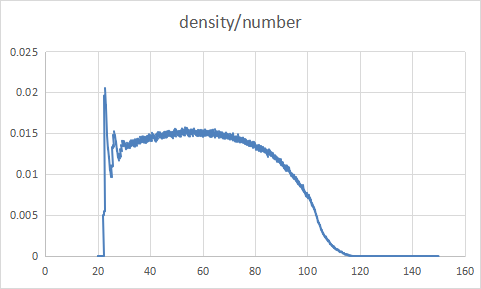
I wonder if this is correct. Shouldn’t the density of liquid water be about 1g/cm3 at 300K? The density oscillations on the solid surface should be higher than 1, right?
You get the density of the volume element that you define and for 1-d binning of a droplet that contains a lot of vacuum hence the low density values.
Restricting such a calculation additionally by the surface of the droplet is very tricky business since you have point particles, so you need some triangulating procedure and some assumption of the “volume” of your point particles.
Also, since you are using mW, you get the density of mW, not the density of water. You should read the original mW papers to find out what that is. Regarding Axel’s point about indeterminate volume, you could do a 3d binning of the simulation volume, apply a threshold on particle count for each 2d layer of bins, and then average over the remainder. That will give you a fairly robust 1d density profile. You could also combine the 3d binning to estimate layer volume with your existing 1d binning.