Hi,
I have some confusion regarding to the formation energy and space group:
In some materials by looking at their formation energy and their structure, they have exactly the same formula and space group from the downloaded CIF, but different formation energy.
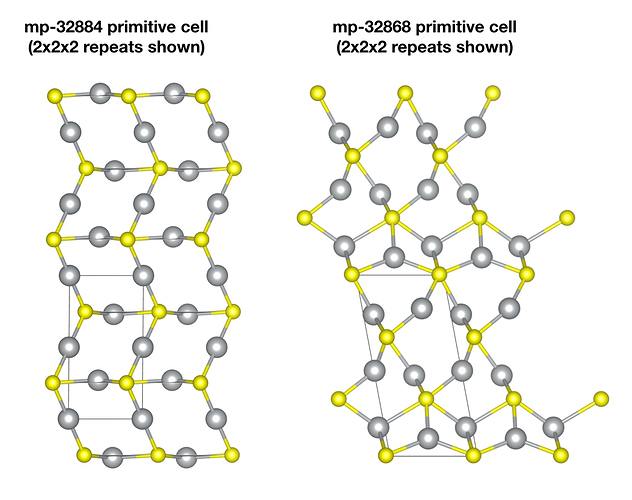
Taking the following two with formula Ag2S as an example.
-
https://materialsproject.org/materials/mp-32868/, formation energy = -0.227
-
https://materialsproject.org/materials/mp-32884/, formation energy = -0.274
What is strange to me is on the web page of the two links, the first one has space group P1[1], the second one has C2/m [12].
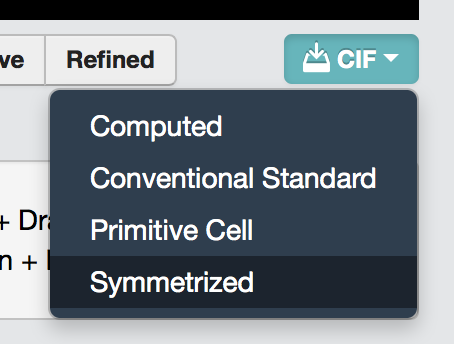
However, since I used their API so what I downloaded are the two cifs by selecting Structure Type = Conventional Standard and clicking on the CIF download button with Primitive cell.
I was curious why the space group on downloaded CIF file is different than the one in webpage? How does it makes difference in physics in such case?
Thanks in advance.
1 Like
Hi @Hemanta,
This is an interesting question! I can understand your confusion.
First, to clarify, these are different polymorphs. To use your Ag2S example, if you download the primitive cell for mp-32868 and the cell for mp-32884 and visually inspect them, you will see they are quite different crystal structures. This is why they have different formation energies, different band gaps, etc.
However, the confusion arises because the CIF file you downloaded reports both primitive cells as having symmetry P1. This is because no symmetry analysis is performed on these structures.
To explain further, there are multiple ways of representing the same crystal structure. You can use a space group (e.g. C2/m) with a basis of atoms, and then under the symmetry operations of that space group you can calculate all equivalent positions of those basis atoms until you have constructed your unit cell. Alternatively, the same crystal can be represented using simply P1 symmetry (i.e. with no additional symmetry operations) and then list every atom in your crystal’s unit cell directly.
When we perform calculations on a crystal structure, we input the crystal using just a list of atoms and the associated unit cell lattice vectors. Notably, the space group is not entered. All our calculation inputs implicitly assume P1 symmetry. It is only later that we perform a symmetry analysis to calculate the space group of our crystal, and that’s what you see reported on the website. Therefore, you can trust the space group displayed on the website to be accurate.
However, for the CIF file you downloaded, we have not performed a symmetry analysis, so the crystal is listed as just P1. Note however that this is simply a lack of analysis: if you plot the atomic positions, you’ll see all the relevant symmetries are still present.
If you would like a CIF file with a symmetry analysis performed (i.e. displaying the correct spacegroup information), just select the ‘Symmetrized’ download option instead.
I hope this helps!
Best,
Matt
2 Likes
Hi mkhorton,
I have some confusion regarding to Primitive CIF and Symmetrize CIF. I was using angles, primitive lattice vectors (abc) and coordinates from Primitive CIF for some statistical analysis, now I am afraid of following:
As abc, angles are not same not same in Primitive CIF and Symmetrized CIF, am I doing something wrong by using those values from Primitive CIF? Does the Physics as a whole or lets say electronic properties of the system in both CIF remains same? Even there are different number of atoms in two CIF, does it makes any difference in physics of the system?
Thanks in advance.
Hi @Hemanta,
am I doing something wrong by using those values from Primitive CIF?
This depends on the exact question you’re trying to answer, so I can’t help much here. This may be fine, or it may not.
Does the Physics as a whole or lets say electronic properties of the system in both CIF remains same? Even there are different number of atoms in two CIF, does it makes any difference in physics of the system?
Yes, the underlying physics is the same regardless of how you define your unit cell. The electronic and mechanical properties are the same (e.g. band gap, bulk modulus). The ‘real’ crystal is infinite in extent, how we choose to define a ‘repeat’ unit is entirely arbitrary, although generally certain conventions are followed as to what unit cell is to be used.
However, this does have some consequences for our analysis. For example a band structure calculation performed in a non-primitive cell will have an unconventional reciprocal lattice, band folding, etc. So there are subtle issues that can be encountered in our analysis of data from non-primitive cells, and it is often much more convenient to use primitive cells for this reason. Likewise, structural properties such as an elastic tensor may be potentially misleading for unconventional unit cells since they’ll be referenced to unconventional axes.
This is quite a broad topic to explain well here, I would recommend a textbook such as ‘Band Theory and Electronic Properties of Solids’ (Singleton) or ‘Introduction to Solid State Physics’ (Kittel) if you’d like more information.
Best,
Matt
1 Like