Hello matsci community,
I try to produce a structure factor with ovito that looks similar to this:
https://www.researchgate.net/publication/335722612/figure/fig2/AS:801569612259328@1568120496200/a-Experimental-scattering-data-for-PNIPA-microgels-obtained-by-SLS-and-SAXS-collapsed.ppm
The system that I use was created with the same insilico synthesis protocoll so it should have a similar structur factor (as on the right side of the linked picture). Is consists of about 40 thousand beads, connected with fixed springs to form a network structure. The equilibrium distance between neighbouring beads is about 1.0 and the diameter of the micogel sphere is about
70:
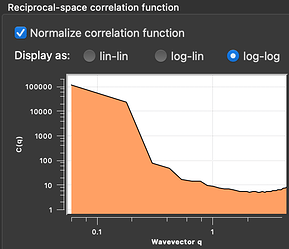
This is the result for a fft grid space of about 0.5 (method from Spatial correlation function — OVITO User Manual 3.7.6 documentation). I can not go much lower or ovito crashes due some memory allocation error after using about 96 percent of my memory. I also tried to vary the cutoff radius (3 to 35) and the number of neighbor bins (50 to 50000) with almost the same result. Direct summation did not seem to make a difference as well.
Is it possible to get the task done with ovito? is there another postprocessing tool to calculate the structure factor of such a system. As far as I read the fourier transformation for bigger systems seems to work with gpu acceleration. Does anyone have some insights on this topic?
I think this might be related to this discussion about the existing limit on the number of FFT grid cells.
Hi!
What is the size of simulation box around the beads? Is the box much larger than the structure or is it tightly fit?
I can take a look at this problem to see which resolution can be achieved with OVITO and whether there is room for further improvement. Would you mind sharing your simulation data with us?
-Alex
The box is 70x70x60, tightly fit. A similar microgel structure can be found in the package here (microgel.dat): Modified LAMMPS fix_bond_create module
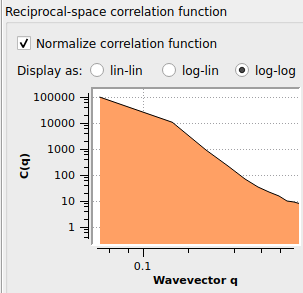
Thanks. I downloaded the data file containing the microgel structure. After turning off periodic boundary conditions for the box, the reciprocal-space correlation function I get for a grid spacing of 0.5 and with windowing looks like this:
Without windowing, it looks almost like yours, yes.
Now regarding the figure from the literature that you referenced above: Do you think the scale of the wave vector axis is equivalent to the one in OVITO? I am not entirely sure what “in MD units” means in this case.
But more importantly perhaps, after I looked at the original paper, I got the impression that the authors may really have employed a different calculation method for the structure factor. This is the relevant part from the method section:
A difference that could also play an important role is the fact that the authors have computed the structure over 50 conformations simultaneously, which could mean that the resulting curve contains considerably more details.
Oh, of course. Maybe I can use the Diffraction Module of the freud tool: Diffraction Module — freud 2.10.0 documentation