Dear LAMMPS team,
I would appreciate your insight into why I’ve been running into this runaway temperature problem while using LAMMPS’s aspherical methods. In this simulation, I use the settings in the example ‘ellipse’ in LAMMPS package (in.ellipse.gayberne, version 15Apr2020); my full script is at the end of this message. I set only one type of ellipsoid in the system and keep the mass and volume of the ellipsoid to be the same as in the original example. I varied the aspect ratio of the ellipses between 1 and 3, which interestingly led to very different behaviors in the NVE ensemble.
I ran the simulation in three stages: 100000 steps of nve/limit to eliminate/mitigate overlaps in case any were present, 100000 steps of nvt/asphere to equilibrate the temperature, and then 1000000 steps of nve/asphere (during which I hoped the temperature would be stable).
Unfortunately this is not what I found. I plot below the temperature in NVT and NVE. When the atoms are perfectly spherical (aspect ratio of 1), the temperature remains stable during NVE, with fluctuations that are roughly on the order I would expect from stat mech. However, when I changed the aspect ratio (x) of the ellipsoid to be 3:1, the temperature continuously grows in the NVE ensemble (left side of the green line is NVT ensemble and right side is NVE).
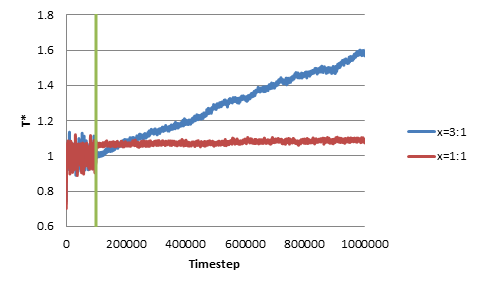
The growing trend can also be observed when we change the original non-dimensional temperature to be 0.5 or 5. In addition, I’ve tried changing the length of the NVT run as well as changing the damping parameter (0.1 through 10), but the trend of growing temperature still persists. As an additional note, I’ve tried some extremely long NVE runs, and the temperature increase persists for the entire duration after the switch from NVT to NVE.
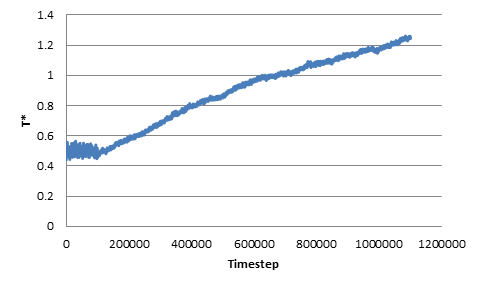
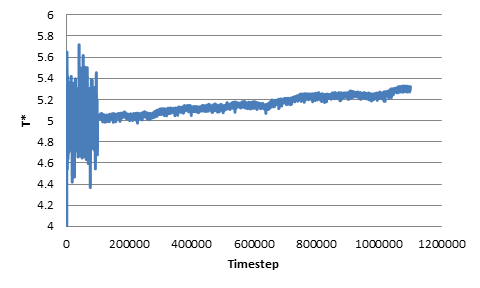
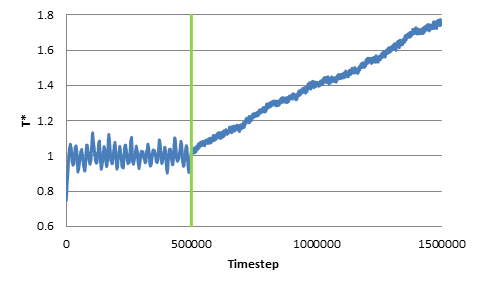
As a sanity check, I’ve plotted the energy change during the NVE run, and confirmed that indeed the kinetic energy (and thus the total energy) keeps increasing in the NVE ensembles. Thus I suspect that I have either misused the aspherical integrators or, perhaps, that there is a bug in these integrators.
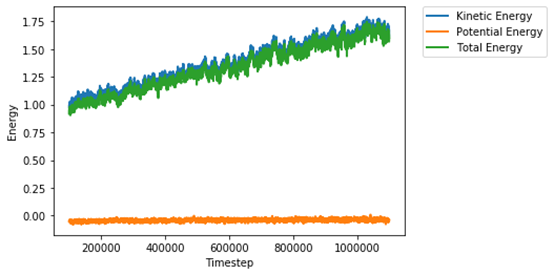
In summary, the problem we find is that when we use the NVE ensemble to collect data for aspherical atoms, we observe a stark trend of temperature increase, which cannot be solved by changing equilibration time, damping parameter, or original temperature. I would greatly appreciate any ideas that anybody has on this matter.
Sincerely,
Shuyuan Wang
The full script of the simulation:
# GayBerne ellipsoids in LJ background fluid
units lj
atom_style ellipsoid
dimension 2
lattice sq 0.02
region box block 0 20 0 20 -0.5 0.5
create_box 1 box
create_atoms 1 box
set group all type/fraction 1 0.1 95392
set type 1 mass 1.0
set type 1 shape 2.08 0.693 0.693
set group all quat/random 18238
compute rot all temp/asphere dof all
velocity all create 1 187287 loop geom
pair_style gayberne 1.0 3.0 1.0 4.0
pair_coeff 1 1 1.0 1.0 1 1 1 1 1 1 2.5
neighbor 0.8 bin
thermo_style custom step c_rot epair ke pe etotal press vol
thermo 100
timestep 0.002
compute orient all property/atom quatw quati quatj quatk
compute shape all property/atom shapex shapey shapez
fix 1 all nve/limit 0.01
run 100000
reset_timestep 0
unfix 1
fix temp all ave/time 1 1 100 c_rot file temp.profile
fix 1 all nvt/asphere temp 1 1 1
run 100000
unfix 1
fix 1 all nve/asphere
dump 1 all custom 100 dump.ellipse.gayberne.lammpstrj &
id type x y z c_orient[1] c_orient[2] c_orient[3] c_orient[4] c_shape[*]
run 1000000