The NVE integrator does not conserve total energy when a dihedral potential is applied to a toy polymer system

NateHess · November 9, 2023, 10:13pm

My question has to do with the total energy conservation of the NVE integrator in LAMMPS with a dihedral potential applied to a short toy polymer. I am using the Aug 2023 distribution of LAMMPS.

Here is the system I am considering:

There are four atoms connected in a chain with harmonic bonds (1 bonds 2, 2 bonds 3, 3 bonds 4). These atoms interact with a LJ potential (FENE bonds are on such that only 1-2 pairwise interactions are excluded). Additionally, there is a dihedral potential applied to this polymer chain. The system is initialized with a velocity corresponding to 300 Kelvin.

I am observing that when I simulate the system with a dihedral potential on (I tested a quadratic dihedral potential and a harmonic dihedral potential), total energy is not conserved (it increases with time). I tested a variety of systems with different boundary conditions and various potentials turned on and off. Here are those systems:

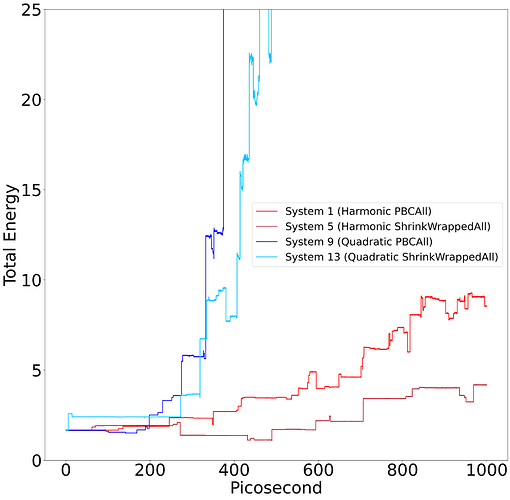
System 1 – Harmonic PBCAll:
Harmonic dihedral potential, LJ potential, harmonic bonds, periodic boundary conditions. Energy is not conserved.

System 2 – Harmonic PBCBondedOnly:
Harmonic dihedral potential, harmonic bonds, periodic boundary conditions. Energy is not conserved.

System 3 – Harmonic PBCDihedralOnly:
Harmonic dihedral potential only, periodic boundary conditions. Energy is not conserved.

System 4 – Harmonic PBCNoDihedral:
LJ potential, harmonic bonds, periodic boundary conditions. Energy is conserved.

System 5 – Harmonic ShrinkWrappedAll:
Harmonic dihedral potential, LJ potential, harmonic bonds, shrink wrapped boundary conditions. Energy is not conserved.

System 6 – Harmonic ShrinkWrappedBondedOnly:
Harmonic dihedral potential, harmonic bonds, shrink wrapped boundary conditions. Energy is not conserved.

System 7 – Harmonic ShrinkWrappedDihedralOnly:
Harmonic dihedral potential only, shrink wrapped boundary conditions. Energy is conserved.

System 8 – Harmonic ShrinkWrappedNoDihedral:
LJ potential, harmonic bonds, shrink wrapped boundary conditions. Energy is conserved.

System 9 – Quadratic PBCAll:
Quadratic dihedral potential, LJ potential, harmonic bonds, periodic boundary conditions. Energy is not conserved.

System 10 – Quadratic PBCBondedOnly:
Quadratic dihedral potential, harmonic bonds, periodic boundary conditions. Energy is not conserved.

System 11 – Quadratic PBCDihedralOnly:
Quadratic dihedral potential only, periodic boundary conditions. Energy is not conserved.

System 12 – Quadratic PBCNoDihedral:
LJ potential, harmonic bonds, periodic boundary conditions. Energy is conserved. This is a duplicate of system 4.

System 13 – Quadratic ShrinkWrappedAll:
Quadratic dihedral potential, LJ potential, harmonic bonds, shrink wrapped boundary conditions. Energy is not conserved.

System 14 – Quadratic ShrinkWrappedBondedOnly:
Quadratic dihedral potential, harmonic bonds, shrink wrapped boundary conditions. Energy is not conserved.

System 15 – Quadratic ShrinkWrappedDihedralOnly:
Quadratic dihedral potential only, shrink wrapped boundary conditions. Energy is conserved.

System 16 – Quadratic ShrinkWrappedNoDihedral:
LJ potential, harmonic bonds, shrink wrapped boundary conditions. Energy is conserved. This is a duplicate of system 8.

Each of these systems are in the dropbox link I have included here with inputs, configuration files, potential files, trajectories, and log files:

The files are labelled according to the title after System # – FolderTitle.

My original expectation before running these simulations was that if all the energy functions were well-posed and their forces were derived properly, energy should be conserved (given a sufficiently small time step and relatively small forces). Because I am not seeing that, I have a few questions about the behavior I am observing:

Why does the NVE integrator not conserve energy when a dihedral potential is applied (except in the case of a dihedral potential applied to a polymer chain with shrink wrapped boundary conditions and no other potentials)?
Why is there a significant difference in the rate of total energy increase between the same system simulated with PBCs versus shrink wrapped boundary conditions? The boundary conditions for the PBCs should be a box that is large enough such that periodic images do not interact (260^3 cubic angstroms versus a chain that at full stretch is ~12 angstroms).

To motivate question 2, I have included a graph of the total energy in the systems 1, 5, 9, and 13. If there are any additional questions about my simulations, please let me know. Any insight would be extremely helpful.

As a side note: I ran system 1 at a timestep of 0.1 femtoseconds and the behavior was similar to the 10 femtosecond timestep I was using in the prior simulations. Those files can be found here:

srtee · November 9, 2023, 11:10pm

Thanks for reporting this – we appreciate the effort that has gone into thoroughly trying various combinations of settings.

For accessibility purposes, could you add a post on this thread with the text of some inputs you used – let’s say systems 1, 6, and 7? If you include the text between triple backticks

```
like this
```

the forum software will enable code formatting (monospace font, verbatim special symbols and scroll bars where needed). This will help more people look at your code and give feedback. (For example, I’m typing this on a phone during my morning commute, so I’m quite wary of diving into your Dropbox link, even though I’m sure it’s very well organised.)

If particle masses are set in your data files rather than the input scripts, please state those as well. A description of the initial geometry’s angles and dihedrals would also help.

Additionally, the plot in your initial post is not showing for me – I see a “broken link” symbol instead.

I am very much interested in getting to the bottom of this with you.

NateHess · November 9, 2023, 11:46pm

Thanks for your reply! I can absolutely do what you have requested.

For every system, the bond angles and dihedral angle (in the initial configuration) is as follows:

Bond Angle 1: 84.36 degrees (1.472 rad)
Bond Angle 2: 89.21 degrees (1.557 rad)
Dihedral Angle: 11.41 degrees (0.199 rad)

The choice for initial placement was relatively random. I chose numbers such that the system didn’t begin in a straight chain (in case there are instabilities for an undefined dihedral angle, although the source code has safe guards against such configurations).

Additionally, here are the inputs for system 1, 6, and 7. The input scripts and configuration files are identical, so I only include them one time. Below that, I have included my potential files for each of systems 1, 6, and 7.

Input Script:

variable temperature equal 300
variable randomSeed equal 1234

units       real
dimension   3
boundary    p p p
atom_style  full

read_data       config.dat

include potentials.dat

velocity        all create ${temperature} ${randomSeed}

special_bonds fene

neighbor  3.5 multi

timestep        10

min_style       fire
timestep        0.0000001
minimize 0.0 1.0e-8 1000 100000
timestep        0.00001
minimize 0.0 1.0e-8 1000 100000
timestep        0.1
minimize 0.0 1.0e-8 1000 100000
timestep        10
minimize 0.0 1.0e-8 1000 100000

neigh_modify    every 5 delay 0

velocity        all create temperature randomSeed

fix             fxnve   all nve

thermo          10
thermo_style    custom step pe ke temp etotal edihed epair  press
thermo_modify   flush yes

dump            1 all custom 1000 result.lammpstrj id mol type q x y z

run             1000000

write_data      final-structure.dat nocoeff

Configuration File

LAMMPS data file

4 atoms
3 bonds
1 dihedrals

1 atom types
1 bond types
1 dihedral types

-130.000000   130.000000  xlo xhi
-130.000000   130.000000  ylo yhi
-130.000000   130.000000  zlo zhi

Masses

   1 100.0000

Atoms

1 1 1 0.000000 0.200000	0.000000	0.000000
2 1 1 0.000000 4.000000	0.800000	0.000000
3 1 1 0.000000 4.000000	4.000000	0.600000
4 1 1 0.000000 8.000000 4.000000	0.300000

Bonds

1 1 1 2
2 1 2 3
3 1 3 4

Dihedrals

1 1 1 2 3 4

System 1 Potential File

# Styles
pair_style  lj/cut 10.0
bond_style harmonic
dihedral_style harmonic

# Coefficients
pair_coeff * * 0.5 2.0 
bond_coeff 1 9.600 3.81 
dihedral_coeff 1 0.5 1 1

System 6 Potential File

# Styles
#pair_style  lj/cut 10.0
bond_style harmonic
dihedral_style harmonic

# Coefficients
#pair_coeff * * 0.5 2.0 
bond_coeff 1 9.600 3.81 
dihedral_coeff 1 0.5 1 1

System 7 Potential File

# Styles
#pair_style  lj/cut 10.0
#bond_style harmonic
dihedral_style harmonic

# Coefficients
#pair_coeff * * 0.5 2.0 
#bond_coeff 1 9.600 3.81 
dihedral_coeff 1 0.5 1 1

Finally, here is the graph I was trying to display. I am not quite sure why my formatting was rejected in the original post, but I also see a broken link symbol. Hopefully this one works.

I am very happy to post more details on the other simulations I ran. I will refrain from doing that in this post, however, to avoid unnecessary clutter on the thread and because they are in the dropbox link.

srtee · November 10, 2023, 10:09am

Since you haven’t specified any angle potentials, the dihedral by itself is very “floppy”. With both 1-3 and 1-4 short-range interactions enabled, this is probably resulting in a “folded-up” polymer where (for example) bead 1 sticks to bead 3 and bead 2 to bead 4. The dihedral potential is probably unstable under this setup.

As a test, you may want to try using a purely-repulsive potential between beads – such as WCA (LJ cut off at the energy minimum) or a Buckingham potential with no attractive term.

NateHess · November 10, 2023, 3:14pm

Interesting hypothesis! I went ahead and tested a WCA potential and a few other conditions. I have enumerated them below as systems 17 through 21. Hopefully they can begin to shed some light on this behavior.

System 17 – WCA Potential
This system has a harmonic dihedral potential, a harmonic bond potential, and a WCA potential. The potential file is listed below (the input and configuration files are listed as my previous post). Energy is not conserved for this system.

# Styles
pair_style  lj/cut 2.245
bond_style harmonic
dihedral_style harmonic

# Coefficients
pair_coeff * * 0.5 2.0
pair_modify shift yes
bond_coeff 1 9.600 3.81 
dihedral_coeff 1 0.5 1 1

System 18 – Longer Chain No FENE
This system has a harmonic dihedral potential, a harmonic bond potential, and an LJ potential. I wanted to test a system where 1-2, 1-3, and 1-4 don’t interact so I used special bonds LJ 0.0, 0.0, 0.0. I have included the potential and configuration file below. The input file is identical to the previous ones. Energy is not conserved in this system.

# Styles
pair_style  lj/cut 10.0
bond_style harmonic
dihedral_style harmonic

# Coefficients
pair_coeff * * 0.5 2.0
special_bonds lj 0.0 0.0 0.0
bond_coeff 1 9.600 3.81 
dihedral_coeff 1 0.5 1 1

LAMMPS data file

8 atoms
7 bonds
5 dihedrals

1 atom types
1 bond types
1 dihedral types

-130.000000   130.000000  xlo xhi
-130.000000   130.000000  ylo yhi
-130.000000   130.000000  zlo zhi

Masses

   1 100.0000

Atoms

1 1 1 0.000000 0.200000	0.000000	0.000000
2 1 1 0.000000 4.000000	0.800000	0.000000
3 1 1 0.000000 4.000000	4.000000	0.600000
4 1 1 0.000000 8.000000 4.000000	0.300000
5 1 1 0.000000 12.20000	4.000000	0.000000
6 1 1 0.000000 12.00000	0.800000	0.000000
7 1 1 0.000000 16.00000	0.300000	0.600000
8 1 1 0.000000 16.00000 4.000000	0.300000

Bonds

1 1 1 2
2 1 2 3
3 1 3 4
4 1 4 5
5 1 5 6
6 1 6 7
7 1 7 8

Dihedrals

1 1 1 2 3 4
2 1 2 3 4 5
3 1 3 4 5 6
4 1 4 5 6 7
5 1 5 6 7 8

Next, I wanted to try the 4 atom system with a bond angle on and a regular LJ potential. I got very interesting results.

System 19 – Bond Angle Included
This system includes a harmonic dihedral potential, a harmonic bond angle potential, and a harmonic bonded potential with a LJ potential. The configuration file is identical to that in my previous post (4 atoms) and the input file is unaltered. The potential file is below. For this system, energy is conserved.

# Styles
pair_style  lj/cut 10.0
bond_style harmonic
angle_style harmonic
dihedral_style harmonic

# Coefficients
pair_coeff * * 0.5 2.0
bond_coeff 1 9.600 3.81 
angle_coeff 1 0.5 30
dihedral_coeff 1 0.5 1 1

I next wanted to see what would happen if I removed pairwise interactions from this system which conserves energy.

System 20 – Bond Angle Included No Pair Potential
This system includes a harmonic dihedral potential, a harmonic bond angle potential, and a harmonic bonded potential. The potential file is below. For this system, energy is not conserved.

# Styles
#pair_style  lj/cut 10.0
bond_style harmonic
angle_style harmonic
dihedral_style harmonic

# Coefficients
#pair_coeff * * 0.5 2.0
bond_coeff 1 9.600 3.81 
angle_coeff 1 0.5 30
dihedral_coeff 1 0.5 1 1

System 21 – Bond Angle Included No Dihedral Potential
Finally, I wanted to see what would happen if I removed the dihedral potential from system 20. In this system, there is only a bonded potential and a bond angle potential. The potential file is below. Here, energy is conserved.

# Styles
#pair_style  lj/cut 10.0
bond_style harmonic
angle_style harmonic
#dihedral_style harmonic

# Coefficients
#pair_coeff * * 0.5 2.0
bond_coeff 1 9.600 3.81 
angle_coeff 1 0.5 30
#dihedral_coeff 1 0.5 1 1

To provide more information, I am plotting the behavior of the potential energy for all these systems. It is curious that in the systems where the energy is not conserved, it appears that the system jumps up in energy suddenly as if there is some discontinuity. There definitely shouldn’t be a discontinuity, however, for the harmonic dihedral potential as cosine is periodic. Very interesting behavior. Does anyone have any insights?

Finally, here is the dropbox with all my results. Feel free to browse. Additionally, please keep providing suggestions of systems I can run that might provide more information. Happy to keep simulating to get to the bottom of this.

srtee · November 10, 2023, 8:07pm

Well I was wrong (or incomplete) on the role of pairwise interactions – but the straightforward explanation still seems to be that specifying a dihedral potential without angle potentials is mechanically unstable. After all, the dihedral angle is ill-defined when a chain becomes completely straight.

You should try visualising your trajectory to understand exactly what conformations are associated with the sudden energy jumps.

NateHess · November 10, 2023, 10:51pm

Great suggestion! I have implemented a test in the source code to probe this possibility. The results are that it appears to only explain this behavior in specific cases. Let me explain.

Take the harmonic dihedral potential, for example. I have modified the source code to print when the vectors defining the two planes in the dihedral approach zero (vector A: rij cross rkj and vector B: rjk cross rlk). The exact alteration I made to the source code is as follows:

if (rasq < 0.1) utils::logmesg(lmp,"\n vector A is small ");
if (rbsq < 0.1) utils::logmesg(lmp,"\n vector B is small ");

The compute function in the source code for dihedral_harmonic.cpp then looks like

void DihedralHarmonic::compute(int eflag, int vflag)
{
  int i1, i2, i3, i4, i, m, n, type;
  double vb1x, vb1y, vb1z, vb2x, vb2y, vb2z, vb3x, vb3y, vb3z, vb2xm, vb2ym, vb2zm;
  double edihedral, f1[3], f2[3], f3[3], f4[3];
  double ax, ay, az, bx, by, bz, rasq, rbsq, rgsq, rg, rginv, ra2inv, rb2inv, rabinv;
  double df, df1, ddf1, fg, hg, fga, hgb, gaa, gbb;
  double dtfx, dtfy, dtfz, dtgx, dtgy, dtgz, dthx, dthy, dthz;
  double c, s, p, sx2, sy2, sz2;

  edihedral = 0.0;
  ev_init(eflag, vflag);

  double **x = atom->x;
  double **f = atom->f;
  int **dihedrallist = neighbor->dihedrallist;
  int ndihedrallist = neighbor->ndihedrallist;
  int nlocal = atom->nlocal;
  int newton_bond = force->newton_bond;

  for (n = 0; n < ndihedrallist; n++) {
    i1 = dihedrallist[n][0];
    i2 = dihedrallist[n][1];
    i3 = dihedrallist[n][2];
    i4 = dihedrallist[n][3];
    type = dihedrallist[n][4];

    // 1st bond

    vb1x = x[i1][0] - x[i2][0];
    vb1y = x[i1][1] - x[i2][1];
    vb1z = x[i1][2] - x[i2][2];

    // 2nd bond

    vb2x = x[i3][0] - x[i2][0];
    vb2y = x[i3][1] - x[i2][1];
    vb2z = x[i3][2] - x[i2][2];

    vb2xm = -vb2x;
    vb2ym = -vb2y;
    vb2zm = -vb2z;

    // 3rd bond

    vb3x = x[i4][0] - x[i3][0];
    vb3y = x[i4][1] - x[i3][1];
    vb3z = x[i4][2] - x[i3][2];

    // c,s calculation

    ax = vb1y * vb2zm - vb1z * vb2ym;
    ay = vb1z * vb2xm - vb1x * vb2zm;
    az = vb1x * vb2ym - vb1y * vb2xm;
    bx = vb3y * vb2zm - vb3z * vb2ym;
    by = vb3z * vb2xm - vb3x * vb2zm;
    bz = vb3x * vb2ym - vb3y * vb2xm;

    rasq = ax * ax + ay * ay + az * az;
    rbsq = bx * bx + by * by + bz * bz;
    rgsq = vb2xm * vb2xm + vb2ym * vb2ym + vb2zm * vb2zm;
    rg = sqrt(rgsq);

    if (rasq < 0.1) utils::logmesg(lmp,"\n vector A is small ");
    if (rbsq < 0.1) utils::logmesg(lmp,"\n vector B is small ");

    rginv = ra2inv = rb2inv = 0.0;
    if (rg > 0) rginv = 1.0 / rg;
    if (rasq > 0) ra2inv = 1.0 / rasq;
    if (rbsq > 0) rb2inv = 1.0 / rbsq;
    rabinv = sqrt(ra2inv * rb2inv);

    c = (ax * bx + ay * by + az * bz) * rabinv;
    s = rg * rabinv * (ax * vb3x + ay * vb3y + az * vb3z);

    // error check

    if (c > 1.0 + TOLERANCE || c < (-1.0 - TOLERANCE)) problem(FLERR, i1, i2, i3, i4);

    if (c > 1.0) c = 1.0;
    if (c < -1.0) c = -1.0;

    m = multiplicity[type];
    p = 1.0;
    ddf1 = df1 = 0.0;

    for (i = 0; i < m; i++) {
      ddf1 = p * c - df1 * s;
      df1 = p * s + df1 * c;
      p = ddf1;
    }

    p = p * cos_shift[type] + df1 * sin_shift[type];
    df1 = df1 * cos_shift[type] - ddf1 * sin_shift[type];
    df1 *= -m;
    p += 1.0;

    if (m == 0) {
      p = 1.0 + cos_shift[type];
      df1 = 0.0;
    }

    if (eflag) edihedral = k[type] * p;

    fg = vb1x * vb2xm + vb1y * vb2ym + vb1z * vb2zm;
    hg = vb3x * vb2xm + vb3y * vb2ym + vb3z * vb2zm;
    fga = fg * ra2inv * rginv;
    hgb = hg * rb2inv * rginv;
    gaa = -ra2inv * rg;
    gbb = rb2inv * rg;

    dtfx = gaa * ax;
    dtfy = gaa * ay;
    dtfz = gaa * az;
    dtgx = fga * ax - hgb * bx;
    dtgy = fga * ay - hgb * by;
    dtgz = fga * az - hgb * bz;
    dthx = gbb * bx;
    dthy = gbb * by;
    dthz = gbb * bz;

    df = -k[type] * df1;

    sx2 = df * dtgx;
    sy2 = df * dtgy;
    sz2 = df * dtgz;

    f1[0] = df * dtfx;
    f1[1] = df * dtfy;
    f1[2] = df * dtfz;

    f2[0] = sx2 - f1[0];
    f2[1] = sy2 - f1[1];
    f2[2] = sz2 - f1[2];

    f4[0] = df * dthx;
    f4[1] = df * dthy;
    f4[2] = df * dthz;

    f3[0] = -sx2 - f4[0];
    f3[1] = -sy2 - f4[1];
    f3[2] = -sz2 - f4[2];

    // apply force to each of 4 atoms

    if (newton_bond || i1 < nlocal) {
      f[i1][0] += f1[0];
      f[i1][1] += f1[1];
      f[i1][2] += f1[2];
    }

    if (newton_bond || i2 < nlocal) {
      f[i2][0] += f2[0];
      f[i2][1] += f2[1];
      f[i2][2] += f2[2];
    }

    if (newton_bond || i3 < nlocal) {
      f[i3][0] += f3[0];
      f[i3][1] += f3[1];
      f[i3][2] += f3[2];
    }

    if (newton_bond || i4 < nlocal) {
      f[i4][0] += f4[0];
      f[i4][1] += f4[1];
      f[i4][2] += f4[2];
    }

    if (evflag)
      ev_tally(i1, i2, i3, i4, nlocal, newton_bond, edihedral, f1, f3, f4, vb1x, vb1y, vb1z, vb2x,
               vb2y, vb2z, vb3x, vb3y, vb3z);
  }
}

I then redid systems 1, 2, and 3. For systems 1 and 2, I did indeed see that the ‘jumps’ in energy coincided with the log.lammps file printing either “vector A is small” or “vector B is small” to the screen. So, with a polymer chain that contains multiple types of interactions where the bonded interactions include a dihedral potential without a bond angle potential, a straight chain explains the energy jump. However, I never saw the print statements coincide with a straight chain for system 3 (simulating with only a dihedral potential). To test this further, I increased the range on my print statement to be:

if (rasq < 10.0) utils::logmesg(lmp,"\n vector A is small ");
if (rbsq < 10.0) utils::logmesg(lmp,"\n vector B is small ");

Still, I did not see any prints to the log.lammps that vector A is small or vector B is small. Therefore, I do not believe that the ‘straight chain’ behavior is an explanation for the energy drift of a set of atoms with only a dihedral potential applied. Additionally, it makes sense that a dihedral potential applied to a set of four atoms could never straighten the chain. This leads me to ask, then, why is there an energy drift when I apply only a dihedral potential to such a system? If the potential is conservative, should not the total energy be conserved?

My hypothesis is that it has to do with the PBCs. The shrink wrapped case for a dihedral potential alone applied to four atoms does conserve total energy. My current explanation is that the atoms travel quickly through the periodic boundary conditions when the dihedral angle potential is applied without a constraining bonded potential. Thus, the value of the forces changes discontinuously for the atoms and the system experiences an increase in energy.

My overall takeaway: if you want to isolate the energy drift of a dihedral potential in LAMMPS do it in shrink wrapped boundary conditions. I am currently developing some of my own non-bonded potentials (which led me to this discussion in the first place) and I will use this principle going forward. If the force from a dihedral potential is correctly derived, applying it on a set of four atoms in a shrink wrapped system with no additional potentials will conserve total energy (with very minimal drift due to integration). In PBCs, this may be confounded due to atoms crossing periodic boundaries. Finally, a dihedral potential will be unstable unless it is paired with a bond angle potential that avoids a straight chain case. This is unavoidable because any derivative of a dihedral angle with respect to an atomic position will result in an inverse magnitude of the vectors that define the 2 planes in the dihedral (vectors A and B above).

Thanks for your help in probing this issue!