I’ve been trying to verify the output from the third_order command and ran across a weird issue: the force constants do not seem to follow the correct constraints. The most basic constraint is that force constants are invariant to the order of the index (tensor should be symmetric):
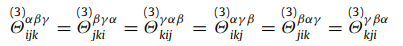
Below I pasted the 6 lines dumped third_order whose first terms should be equal.
The format of the output is i / alpha / j / beta / k gamma=1 gamma=2 gamma=3. With this I am just looking at gamma=1 to keep things simple. I expected all 6 of these to have the first gamma1 term but they do not. I am not sure if I am just interpreting the format wrong or if the output is wrong. Any help would be appreciated!
1 1 2 1 3 20.81668171 0.86736174 -5.20417043
1 1 3 1 2 10.40834086 0.00000000 -14.7451495
2 1 3 1 1 27.75557562 -13.87778781 -3.46944695
2 1 1 1 3 20.81668171 0.86736174 -5.20417043
3 1 1 1 2 10.40834086 0.00000000 -14.74514955
3 1 2 1 1 27.75557562 -13.87778781 -3.46944695
It is very difficult to provide a meaningful response without knowing more details.
For example, it would matter what kind of system you are studying and what kind of potentials you are using and whether you have properly minimized the system before running the third_order command. Since LAMMPS uses floating point math and the third_order command is based on finite differences, it is quite easily possible to have deviations from the ideal case, specifically of not everything else is “perfect” and you are using a potential that uses spline interpolation somewhere.
Since this is a very special command that not many of the LAMMPS developers (and users) have experience with, your best bet for assistance would be to contact the author that contributed the code. Contact info should be in the source code.
1 Like
Yeah I’ll try e-mailing.
The system is FCC at its equilibrium position with 4 unit cells and to be honest it should not matter the symmetry constraints are true regardless. It is effectively a statement of Clairaut’s theorem that derivatives should be interchangeable so the structure should not matter. It also does not matter if it is at equilibrium. And this isn’t really a small deviation it is completely different, hence I think my interpretation is wrong (or the output formatting is wrong).
Hello Ethan,
Axel is quite right about deviations arising due to finite differences.
Sometimes the differences arise from delta-x and/or potential cutoffs.
Please post your input file.
Best,
Charlie
Here’s the input file. I’ll try playing around with the inputs more to see if anything changes.
in.lammps_dynmat_test (1.3 KB)
Thanks!
I’ll see if I get some time to check it out this week, but first thing I would start off with is to change the delta x to 1e-6. Usually the sweet spot for delta x is somewhere around there. Also, you don’t need a skin of 1. Your skin just needs to be bigger than your delta x. Finally, one last thing is do not run the dynamical matrix command before hand, I need to fix a bug where the last movement gets undone.
1 Like
I tried a couple things but could not resolve the issues I was having. Changing the value of dx does have rather drastic effects on the results, but of the 3 cases (1e-6,1e-8, 1e-9) I tried none solved the issue. I’m also a little surprised that the results are so sensitive to the choice of dx. I would have thought if you have a stable configuration that overly small dx would not hurt your results.
Tried another code that uses finite differences & LAMMPS as a force calculator see here. There are no issues with symmetry here and it is really not that sensitive to the choice of dx. I have no clue what is going on (sorry not that helpful I know) but I’m pretty confident something is not right. Whether that is in the code or my input script I don’t know.
Something that’s always been a little suspicious to me is how fast the LAMMPS code runs. I’m not an MPI expert but the implementation in ModeCode and LAMMPS should not differ than much but the runtime is about 100x different.
Try out the input file I just sent over. If it works, then there is a problem with precision on non metal units. Which would make sense in this case.
Drew, the guy who made that dynamical matrix calculator, is a great guy! If you get a chance to use his software do it. The reason the dynamical_matrix command is faster, is because I am not using any library calls and I abuse lammps neighbor lists, this is an extra advantage in the third order calculator.
1 Like
Sounds good I’ll check it out. Thanks for putting some time into this I know you’re long graduated.
I actually met Drew at MRS this Spring, a lot of what I’m trying to do builds off some of his work.
Can confirm ModeCode is not making smart use of LAMMPS neigh lists like Charlie did in the dynamical matrix command style. That would definitely speed things up.
1 Like
Ok so I ran the files you sent me. What did you change it looked the same as what I was doing?
- The dynamical matrices produce basically identical frequencies and also match GULP and my own analytical code so all is well there (always was).
- Using the same input file and commenting out the dynamical matrix line to avoid that bug you mentioned I calculated the third_order force constants. It seems to be better than whatever my input had but it still does not satisfy translation invariance. If I sum all of the values I get ~1 whereas ModeCode is ~1e-6 and analytically it should be 0. This basically means the whole simulation cell feels a net force (whether or not a force of 1 is “large” in real units I do not know).
- Is the LAMMPS implementation not taking advantage of the symmetry of the system and re-calculating every term? Even if it is I don’t really see why the finite differences would return different values for elements which should be identical. They should be different from analytical due to finite differencing errors but I would expect them to all be off by the same amount not different amounts.
- None of that really concerns me all that much, the issue is when I go to smaller values of dx (e.g. 1e-7 which the docs use) everything completely breaks. The sum of the values now is ~13000 which is definitely too large. This does not happen with ModeCode and I’m not really sure why it happens in LAMMPS. Maybe LAMMPS is doing things Float32 and rounding becomes a big problem. I’m not sure.
![]()