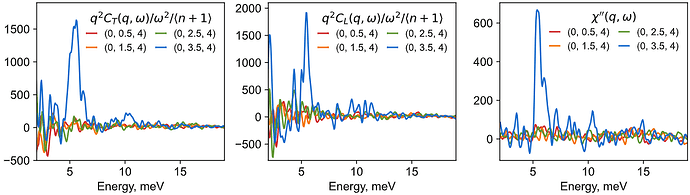
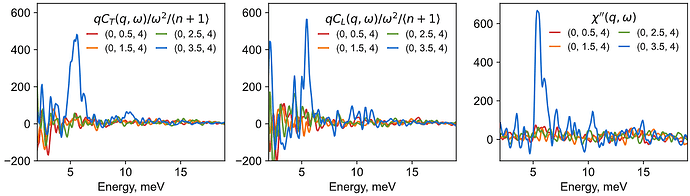
I am attempting to reproduce some of the calculations related to transverse acoustic modes in this paper (their figure 3f in particular) using dynasor. Numbered equation 1 in the dynasor 2 paper relates the dynamic structure factor to the longitudinal current correlation function exclusively: w^2 S(q,w) = q^2 C_L (q,w). I am puzzled by how the first paper claims to simulate the dynamic susceptibility for transverse modes from the structure factor. It would make sense for the dynamic scattering factor to contain both longitudinal and transverse modes, because neutron scattering probes both polarizations. I also tested the above equation from my own simulation analyzed with dynasor, and did not obtain correspondence between spectra of S and C_L versus frequency at specific q-points, although there is approximate correspondence in overall spectral shapes. In my ideal world, I would be able to reconstruct the longitudinal and transverse components of the dynamic structure factor separately. What am I missing, or what could I do to troubleshoot?
Thank you!
-Andrey