Hi all, I am currently trying to figure out the slab energy (calculated as the interaction energy between a central, reference molecule in the slab and all other molecules in the slab) of the basal slab of hexagonal ice in Lammps (version of 19/11/2024) in its initial state at t=0. I have already created the slab, and used atomsk to convert it into a tetragonal cell.
To account for the long-range Couloumbic interactions, I’ve implemented the Ewald sum. I do however find the results quite weird, as it seems that these interactions make my energy smaller and therefore my slab less stable, as can be seen in the picture below. I would not think this realistic, as I would imagine the long range interactions to be stabilizing. I have uploaded images of the energy results, the code, and the slab, respectively, as I can’t upload attachments yet.
It is not correct to compare the results of pair style lj/cut/coul/long with kspace on to the same pair style with kspace off. The Coulomb calculation in the pair style is modified with a damping function so that it can be combined with the kspace calculation for the true Coulomb interaction. You have to compare it to pair style lj/cut/coul/cut with the lj cutoff at the same value and the Coulomb cutoff much larger (you will likely need to increase the space for the neighbor list for that) until you can see it converging to a value. At that point, the two energies should be close to each other.
Thanks for the quick response! If I understand correctly, the calculation of central_recip includes the VdW energy, and both the long range and short range Coulombic energies?
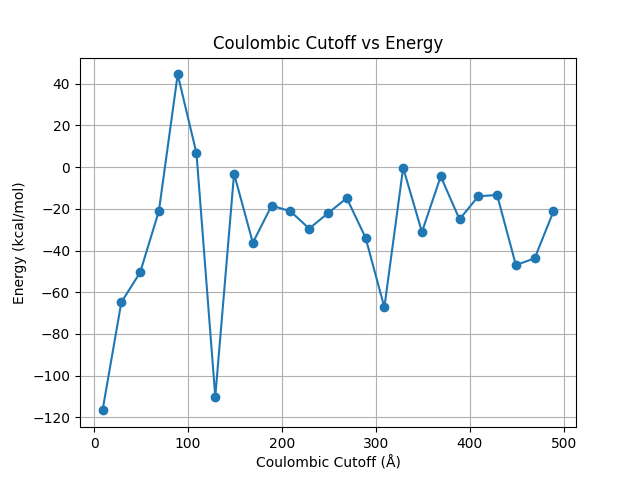
I tried running the system for different Couloumbic cutoffs ranging from 9 to 500, and I do indeed see that the system seems to be converging to a value quite close to the previously obtained -24 kcal/mol.
Would I be able to document my VdW potential and Couloumbic potential separately by using _lj/cut_for the VdW potential, and using the coul/long together with kspace for the Couloumbic potential? In other words, would the sum of these two separately approximate the value of -24 kcal/mol obtained with lj/cut/coul/long?
EDIT: The reason for my last question is that it seems that using coul/long returns the energy for the whole system, and completely ignores the fact that I need the energy between the two previously defined groups.
You are asking questions that are either answered in the LAMMPS manual (I am not repeating the a digested version of the manual for you) or that you should be discussing with your adviser (I am not it).