Dear all,
I want to simulate a stretching CNT and calculate its tensile strength. I need to calibrate the system for more complex geometries. I’d like to reproduce the results in https://www.sciencedirect.com/science/article/pii/S2095034915000525.
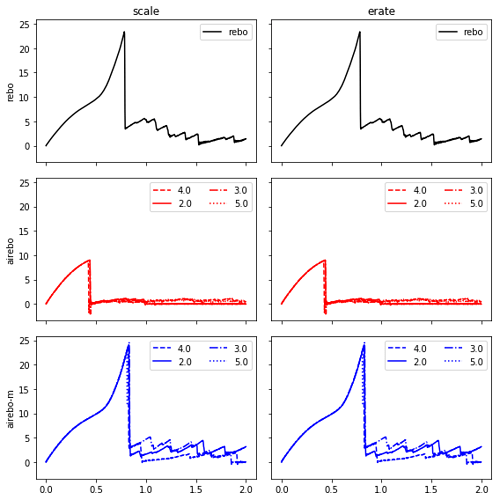
I have produced a 10x10 armchair, 4.8 nm CNT using scikitnano and want to compare rebo vs airebo vs airebo-m for several cutoff parameters with LAMMPS.
I perform energy minimization, followed by a NVE + Berendsen relax and a NPT relax.
Finally I apply a “fix all deform 1 z scale 2”. (I also tested the erate option instead of scale for comparison).
I calculate the strain rate as tot_ratio/tot_time and the stress as follows:
variable dt equal 0.001 #ps
timestep ${dt} #ps
#---------------STRESS-------------------------------------
compute 1 all stress/atom NULL
compute 2 all reduce sum c_1[3]
fix 1 all ave/time 1 100 100 c_2
variable sigmazz equal f_1
##--------------- STRAIN -----------------------
variable Zratio equal 2
variable srate equal ${Zratio}/${Nruns}/${dt} #/ps
variable strain equal step*v_srate*v_dt
###---------------DEFORMATION--------------------------------------
fix 2 all ave/time 1 1 100 v_strain v_sigmazz file deform.dat
dump 1 all atom 100 dump_deform.lammpstrj
fix 3 all npt temp 300 300 0.1 x 0 0 0.5 y 0 0 0.5
fix 4 all deform 1 z scale ${Zratio}
I get at least three problems:
- airebo-m shows no improvement with respect to rebo: there is an un-physical hardening above 5% of strain
- there is almost no difference when changing the LJ cutoff from 2.0 to 5.0 Ang
- generally I’d expect a tensile strength one order of magnitude larger (about 100GPa).
I can imagine there is either a problem in my stress calculation or generally in my minimization/relaxation scheme. Could anyone suggest a solution or improvement?
Please find attached my input and geometry files for reproduction.
Thank you.
input.lammps (3.1 KB)
cnt_10.lmp (33.5 KB)