Please note that the velocity command only sets initial values. The velocity command will factor in the degrees of freedom that are removed by fix shake, but since the output of fix shake is not reliable for the first couple of steps for technical reasons, you are likely creating more problems than solving with your command sequence:
velocity atomsRigid create 300.0 12345
run 0 post no
velocity atomsRigid scale 300.0
What would be important to know is how you are time integrating the system and if you apply a thermostat to the entire system or not.
For example, if you use fix nvt (like in the peptide example) then you have just a single Nose-Hoover thermostat for the entire system (this is usually desired since thermalization is intended to be very weakly coupled). But in this scenario the actual temperature for both the rigid and non-rigid parts depends on how well those two parts can exchange kinetic energy. Most likely, it will take a significant amount of simulation time until this happens.
The alternative would be to use fix nve plus fix langevin where you thermalize individual atoms through random forces balanced by friction. This kind of dissipative thermostat can distribute kinetic energy much more efficiently, but also has much more impact on the trajectory. People often start with this setup until the expected equipartitioning is achieved and then switch to a Nose-Hoover thermostat.
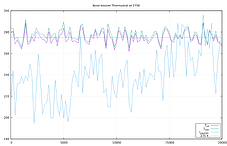
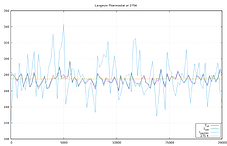
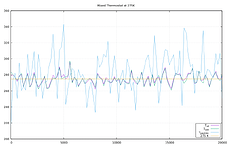
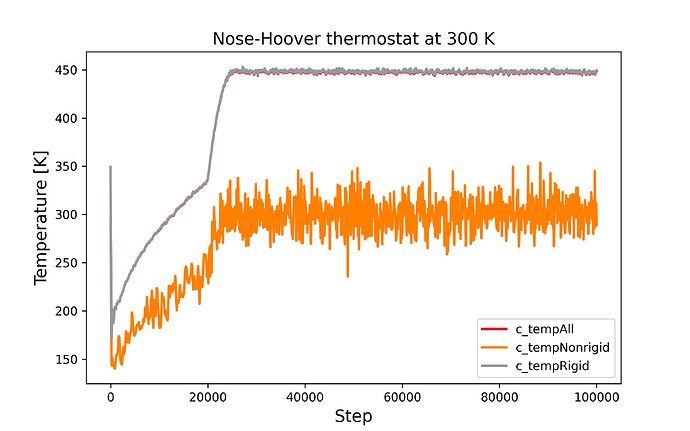
Please see the graphs below for a demonstration. I have modified the “peptide” example from the LAMMPS source distribution, so that fix shake is only applied to the water molecules and then defined separate computes for temperature of all atoms, only the water atoms, and only the peptide atoms. The timestep was reduced to 0.5fs and the length of the run extended to 200000 steps.
Due to no longer having shake constraints on the hydrogen atom bonds in the peptide, the peptide atoms are not in equilibrium at the beginning and equipartitioning of the kinetic energy is not given.
As you can see from the right graph, the peptide atom temperature is lower than the target, but over the course of the simulation they slowly pick up the kinetic energy from surrounding water molecules. Since there are so many more water atoms than peptide atoms, the water temperature is only a little bit affected and fix nvt keeps the total temperature on target, but does nothing to assist the exchange of kinetic energy of the two subsystems.
I’ve then replaced fix nvt with fix nve and fix langevin with the same relaxation time as used in fix nvt. And you can see from the middle graph that the dissipative nature of fix langevin achieves equipartitioning of the temperature between the two subsystems within the first 1000 time steps.
The third graph is a mix where the first 100000 timesteps use Langevin for thermostatting and then second 100000 steps fix nvt. It is quite obvious that running fix nvt will inherit the equipartition of temperatures and not break it again.
Bottom line, getting your system in a proper equilibrium including equipartitioning to kinetic energy, may take some time. Using a dissipative thermostat can help, but one also has to factor in how much it will affect the dynamics and in most cases you want to run production with a (weak!) Nose-Hoover thermostatting. Please keep in mind that how easy the system will balance out itself depends on the geometry and details of the setup and vary by large margins.