Hi all,
I want to calculate the volume of a spherical nano-particle resides inside of a cubical simulation box (see the attached figure) utilizing Voronoi tessellation. My input commands are given below,
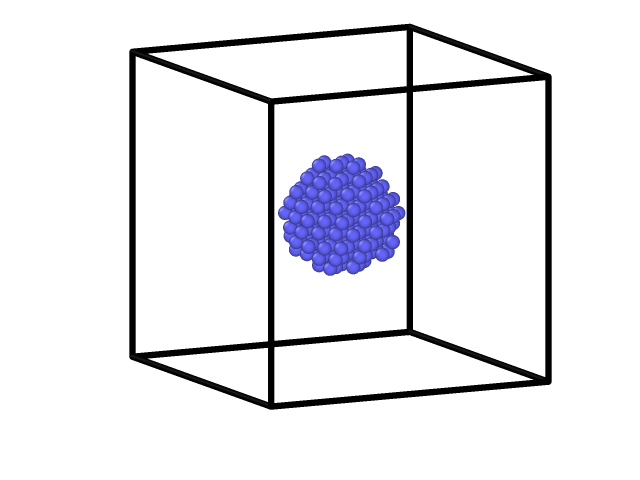
Hi all,
I want to calculate the volume of a spherical nano-particle resides inside of a cubical simulation box (see the attached figure) utilizing Voronoi tessellation. My input commands are given below,

Answering because nobody else has.
I cannot give an idea as to why it’s >2x as big (more worryingly its not constant) - you should get the volume of the box if everything’s done correctly. The voronoi tesselation doesn’t know anything about where the cluster ends and the void begins.
In the mean time, try the scientific method, test it on some simpler systems where things should behave better (non-clustered) and see what you get.
This seems weird indeed. Can you dump the per atom volume and see how the distribution is? Maybe that will help in assessing what goes wrong.
That is indeed odd to get a volume twice as the simulation box... he
volume should be anyway equal or smaller than the simulation box.
But in general, one should not use the Voronoi volume when atoms belong
to a surface. In such a case, it is impossible to build a "voronoi cell"
around the atom, and voro++ (used in Lammps) will stop the volume at the
potential cutoff or ghost atoms distance (don't remember exactly). So,
the "volume" of the surface atom will be anyway wrong. In a more global
point of view, the volume of a surface is an ill defined concept.
Also, I do not see any accurate way to compute the volume of an atomic
sphere within Lammps...