Are there any wall types that can handle ellipsoidal particles such that the ellipsoid orientation is used to determine the separation distance between wall and particle?
Thanks,
David
Are there any wall types that can handle ellipsoidal particles such that the
ellipsoid orientation is used to determine the separation distance between
wall and particle?
nope. at least not in the official lammps distribution.
perhaps somebody on the list here has written one
and has the now the opportunity of his/her 15mins
of fame. 
you could approximate it by a layer of spherical
particles, but that may be a bit costly...
axel.
Something like a fix wall/ellipsoid, similar to wall/colloid
would have to be added ...
Steve
Dear all,
I do not believe the fix I wrote will bring me even 1 min of fame...
However i wrote a fix to compute anisotropic ellipsoid-wall interactions.
Interaction between wall and ellipsoid particle can also be tuned to favor preferential anchoring.
Potential is derived from a 9-3 "Gay Berne" potential.
Derivatives (forces and torques) are calculated following Brenner and Gajdos, Can. J. Chem. 59 p2004-2018 (1980)
I do not promess the fix is bug free.
To use it the syntax is
fix ID group-ID wall/regiongb region-ID Eps_a Eps_b Eps_c EpsilonWall cutoff sigma gamma
where Eps a Eps b Eps c stand for the interaction anisotropy (like in GB potential)
EpsilonWall is the strength factor between wall and particle
cutoff is cutoff
sigma is the size of the pseudo particles of the wall (in sigma 0 unit)
and gamma is the same as for GB potential
If lammps developpers find this (small) piece of code of interest, i can rewrite/change some parts to make it cleaner.
Rémi
fix_wall_region_gb.cpp (14.8 KB)
fix_wall_region_gb.h (2.01 KB)
Dear all,
I do not believe the fix I wrote will bring me even 1 min of fame...
You will always be famous in my eyes.
However i wrote a fix to compute anisotropic ellipsoid-wall interactions.
Interaction between wall and ellipsoid particle can also be tuned to favor
preferential anchoring.
Do you want to post a picture of what you mean?
Hi,
May be my explanations were unclear.
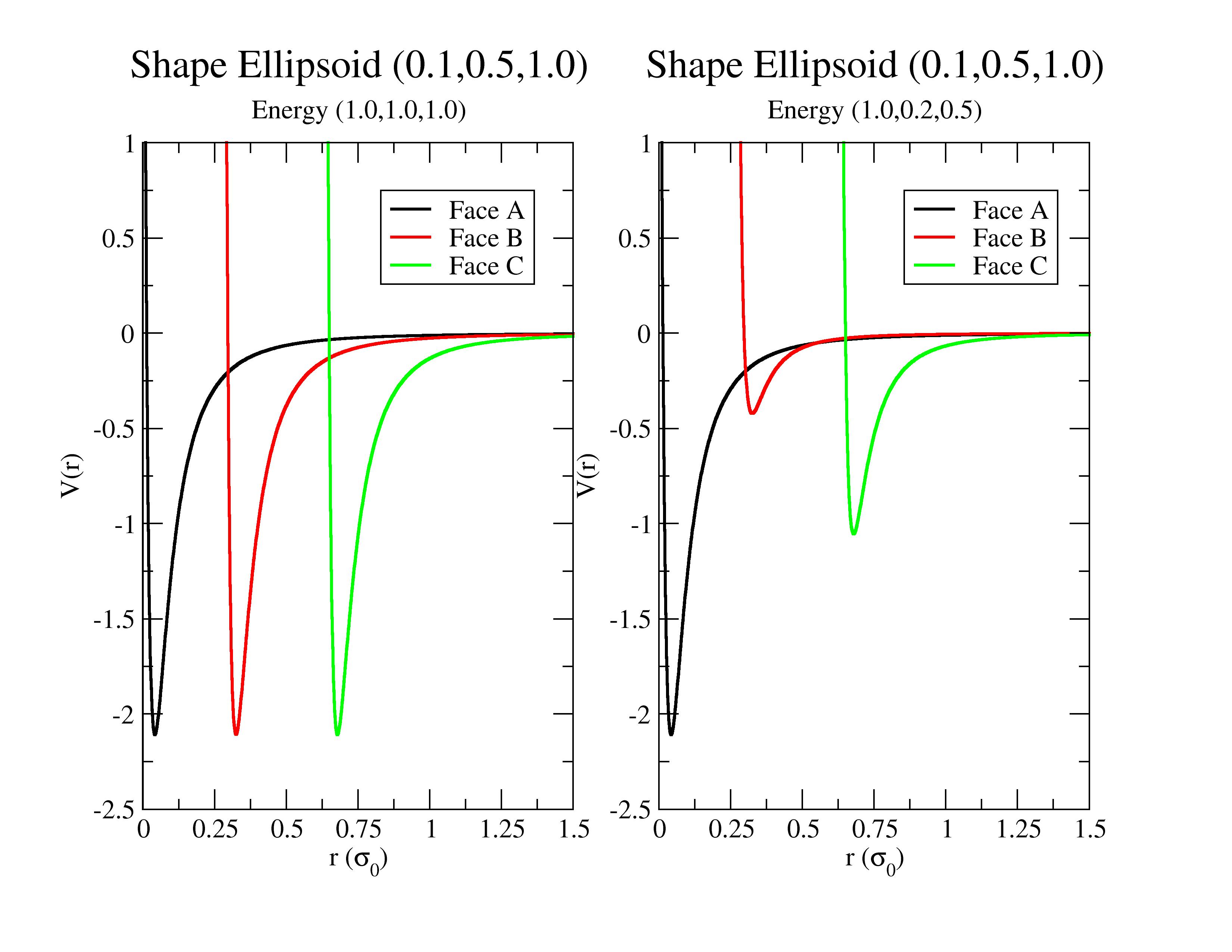
Starting from a biaxial ellipsoidal particles of shape sigma_a sigma_b, sigma_c (in the plots shape is (0.1,0.5,1.0)) and a semi infinite wall, the position of the potential minimum will depend of the face orthogonal to the wall.
But you can also specify different interaction between faces and wall, and hence obtaining preferential anchoring.
In the left figure, i plot resulting potential between biaxial ellipsoid and wall when no preferential anchoring is chosen (in the fix Eps_a=Eps_b=Eps_c=1) for three different position, Face A orthogonal to the wall, Face B orthogonal to the wall and Face C orthogonal to the wall.
For the right figure, i plot resulting potential between biaxial ellipsoid and wall with preferential anchoring (in the fix Eps_a=1.0 Eps_b=0.2 Eps_c=0.5) for three different position, Face A orthogonal to the wall, Face B orthogonal to the wall and Face C orthogonal to the wall.
For all the potential computed, i use a sigma_wall =0.2 where sigma_wall is the diameter of pseudo-particles constituting the wall and epsilon_wall=1.0
I hope it will help
Regards
Rémi
Thanks for working on this. I don't understand
why this fix is derived from fix wall/region and not fix/wall.
Is it meant to work with flat walls, or general regions,
which can be arbitrarily complex surfaces? I don't see
any logic in your fix to figure out how close an ellipsoid
is to an arbitrary curved surface, which sounds hard to
compute.
If it is just for flat, coordinate aligned walls, then I think
you want a file like fix_wall_gb.cpp and it only
needs a wall_particle() method.
Steve
Hi Steve,
In fact i derived this fix from wall/region to work on a precise topic i.e. for confinement in cylinders.
Even if the 9-3 LJ potential arise from the integration of 12-6 LJ potential on a semi-infinite plane it can also be used in a rough approximation for cylindrical confinement mediums if the curvature of the cylinder is "great enough" in comparison to the ellipsoid size.
I only used this fix for plane and cylindrical surfaces, for more complex surface, as you pointed out, it become much more complex to determine the distance of closest approach.
Rémi
I only used this fix for plane and cylindrical surfaces, for more
complex surface, as you pointed out, it become much more complex to
determine the distance of closest approach.
If we add this, I don't see how to prevent users from
using it with an arbitrary region. So unless it is general
purpose or can self-check that it is being used with a valid
geometry, it will cause people problems ... Maybe it makes
more sense to only enable it for flat walls? Which would
mean it should be derived from fix wall, not fix wall/region.
Steve
Hi Steve,
I am agree with your comments, as originally 9-3 potential is developped for flat walls and due to the closest approach problem for arbitraries shapes, it make sense to restrict this fix for flat walls only and so rewrite the fix from fix wall class.
I will rewrite it accordingly to the wall class (when I will have some free time) instead of fix wall/region class.
Rémi
ok - let me know when you have some new code.
I think it would be a nice extension to the wall
options. You are doing this in an analytic sense
so that the ellipsoidal particle "sees" an integrated
form of a pure LJ wall, similar to the 9/3 potential?
Steve
Yes you are right, it is an integration of pure 12-6 LJ potential applied to an ellipsoid of arbitrary shape and with anisotropic energy interaction.
Please keep in mind that the integral form of the potential is not fully analytic but semi-analytic, a fully analytic and exact treatment remains more complex (see Babadi and Ejtehadi Euro phys. Letters 77 p23002 (2007)) but reachable.
Derivation of the semi analytic 9-3 potential is done accordingly to this work (Brenner and Gajdos Can. J. Chem. 59 p2004 (1981)) giving the forces and torques.
Remi