What is the accepatble level of the force error?

hiPhive
1

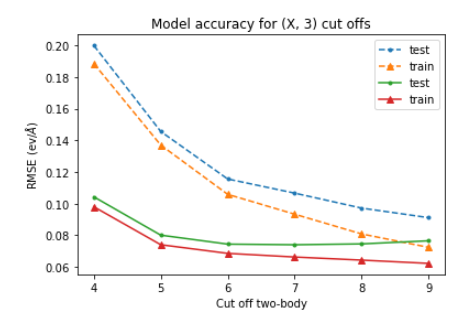
I am trying to get force constant for phono3py calculations. I am wondering what is the target force errors to aim for.

My system is a rutile structured ionic crystal. The force errors that I can get to is around 90- 200 meV/A, using longer ranged 2 body interactions seems to reduce the error towards the lower end (100 meV/A).

In the hiphive paper and other examples, the error on the forces seems to be much lower.

I also tried to separate long-range and short-range interactions following the example in the tutorial, but with the long range substracted the RMSE of the forces increases instead (this is normal?).

Here is an example of the output, using [7, 3] (least-squares):

===================== Optimizer ======================
seed                           : 42
fit_method                     : least-squares
standardize                    : True
n_target_values                : 57600
n_parameters                   : 5173
n_nonzero_parameters           : 5173
parameters_norm                : 616.2072
target_values_std              : 1.406111
rmse_train                     : 0.09352622
rmse_test                      : 0.105613
R2_train                       : 0.9955674
R2_test                        : 0.9944533
AIC                            : -235325.2
BIC                            : -189513.5
train_size                     : 51840
test_size                      : 5760
======================================================

With substracted LR contribution (using a smaller cell size):

===================== Optimizer ======================
seed                           : 199
fit_method                     : least-squares
standardize                    : True
n_target_values                : 34560
n_parameters                   : 5173
n_nonzero_parameters           : 5173
parameters_norm                : 626.8203
target_values_std              : 1.352439
rmse_train                     : 0.2403686
rmse_test                      : 0.2822997
R2_train                       : 0.9683434
R2_test                        : 0.9572655
AIC                            : -78336.59
BIC                            : -35167.43
train_size                     : 31104
test_size                      : 3456
======================================================
2

A rmse vs cutoff plot is typically very helpful. If you aim to extract the true 0K force constants your force error should be essentially zero, the exact tolerance depends on the system. The increase in rmse when applying LRC is odd. Can you show the dispersions with and without LRC? I suspect you need to converge your cutoffs still. Plot the convergence with and without LRC and make sure your second order force constants are good before proceeding to 3rd order.

3

Thanks for your suggestions!

I have found the cause of this. It turns out it was due to the training structures being ordered differently with that in the phonopy supercell.

The following snippet taking from the example ipython notebook

# compute long-range forces due to dipole interactions
ph.set_force_constants(np.zeros((len(supercell), len(supercell), 3, 3)))
dynmat = ph.get_dynamical_matrix()
dynmat.make_Gonze_nac_dataset()
fc_LR = -dynmat.get_Gonze_nac_dataset()[0]

# remove long-range forces from training data
displacements = np.array([s.displacements for s in sc])
M, F = sc.get_fit_data()
F -= np.einsum('ijab,njb->nia', -fc_LR, displacements).flatten()

Would only work if the traning structures in the structure container sc all have the exact same supercell and atomic order compared to that of the supercell. In my case, the latter was not true, e.g. the randomly displacement supercells used for training contains a different order of the atoms. As a result, the LR contribution of the forces are messed up.

To fix it, I used the following function to match the order of the training supercells to that of the phonon py sueprcell, and then add these ordered structures to the StructureContainer.

def match_atomic_order_(atoms: Atoms, atoms_ref:Atoms) -> Tuple[Atoms, List[int]]:
    """
    Reorder the atoms to that of the reference.
    
    Only works for identical or nearly identical structures that are ordered differently.
    Returns a new `Atoms` object with order similar to that of `atoms_ref` as well as the sorting indices.
    """

    # Find distances
    acombined = atoms_ref.copy()
    acombined.extend(atoms)
    new_index = []
    # Get piece-wise MIC distances
    jidx = list(range(len(atoms), len(atoms) * 2))
    for i in range(len(atoms)):
        dists = acombined.get_distances(i, jidx, mic=True)
        # Find the index of the atom with the smallest distance
        min_idx = np.where(dists == dists.min())[0][0]
        new_index.append(min_idx)
    assert len(set(new_index)) == len(atoms), "The detected mapping is not unique!"
    return atoms[new_index], new_index

Now the RMSE does reduce with LR contribution taken out! Maybe this is something to warn people about in the tutorial. This mistake seems very obvious to me now, but it is not the case previously :dizzy_face:.

The other thing I realised is that if I use smaller displacements, the average forces will be smaller, and so does the force fitting error. So probably the acceptable force error should also depends on the magnitudes of the forces in the training structures themselves…

4

For future reference, there is a function in hiphive that does this hiphive.utilities.find_permutation.

The Optimizer also contains and prints the R2-scores (see your post above) which are maybe easier to interpret since its a relative error.
But yes is difficult to say what is acceptable level of RMSE or R2 scores, also because it will depend on how anharmonic the material is. Therefore its typically a good idea to make sure your property of interest (e.g. phonon dispersion or thermal conductivity etc) is well converged with respect to FCs cutoffs and number of training structures.

5

Thanks! With LR-SR separated, I can see that the convergence with two-body cut off becomes much better:

(dashed is without LR-SR separation)
image

I also found that including 4-body cluster (cutoff=[6,3,2.5]) could further reduce the fitting error to about 0.05 eV/A. Given that my end goal is to use the third force constants for phono3py, this this cause problem because now the effects of higher order force constants are not “include” in the third order?

6

I dont think it is necessary to include higher-order terms, but I dont think you need to worry about including fourth-order will drastically change the third-order FCs.
If you really want to get the force-constants corresponding to T=0K, then it could make sense to include small amount of fourth-order.