Why the mechanical properties increase with bulk cell size in LAMMPS(use pbc)?

LAMMPS LAMMPS General Discussion
1

Hi everyone,

I want to determine the size of the bulk cell to be used. I check different bulk cell size.

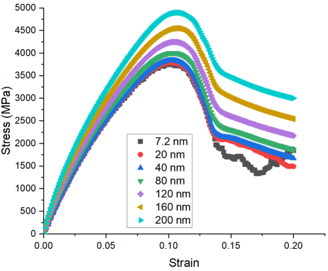
When doing the compression of copper single crystals, except for the size of the bulk cell I used, the other conditions used are the same (periodic boundary conditions are applied). Why do the resulting Young’s modulus and yield strength increase as the bulk cell size increases? Why am I not seeing convergence? Can anyone give me some advice about this? Thank you in advance!

AA

The following are the script I used:

------------------------ INITIALIZATION ----------------------------

units metal
dimension 3
boundary p p p
atom_style atomic
variable latparam equal 3.597

----------------------- ATOM DEFINITION ----------------------------

lattice fcc {latparam} region whole block 0 55 0 55 0 55 create_box 1 whole region upper block INF INF INF INF INF INF units box lattice fcc {latparam} orient x 1 0 0 orient y 0 1 0 orient z 0 0 1
create_atoms 1 region upper

------------------------ FORCE FIELDS ------------------------------

pair_style eam/alloy
pair_coeff * * Cu01.eam.alloy Cu

------------------------- SETTINGS ---------------------------------

compute csym all centro/atom fcc
compute peratom all pe/atom

######################################

EQUILIBRATION

reset_timestep 0
timestep 0.001
velocity all create 300 12345 mom yes rot no
fix 1 all npt temp 300 300 1 iso 0 0 1 drag 1

Set thermo output

thermo 1000
thermo_style custom step pxx pyy pzz pe temp lx ly lz press
run 300000
unfix 1

Store final cell length for strain calculations

variable tmp equal “lx”
variable L0 equal {tmp} print "Initial Length, L0: {L0}"

######################################

DEFORMATION

reset_timestep 0
fix 1 all npt temp 300 300 1 y 0 0 1 z 0 0 1 drag 1
variable srate equal 1.0e10
variable srate1 equal “-v_srate / 1.0e12”
fix 2 all deform 1 x erate ${srate1} units box remap x

variable strain equal “(lx - v_L0)/v_L0”
variable p1 equal “v_strain”
variable p2 equal “-pxx/10000”
variable p3 equal “-pyy/10000”
variable p4 equal “-pzz/10000”

fix def1 all print 100 “{p1} {p2} {p3} {p4}” file Cu_comp_100.def1.txt screen no

Use cfg for AtomEye

dump 1 all cfg 100 dump.comp_*.cfg mass type xs ys zs c_csym c_peratom fx fy fz

dump_modify 1 element Cu
thermo 1000
thermo_style custom step v_strain temp v_p2 v_p3 v_p4 ke pe press

run 20000

2

Firstly, your script has been misformatted because of special characters in it (like $, * and #). Please use backticks to make a non-formatted code block for your script

```
like this.
```

Secondly, you have provided your script for only one box size it seems, and it’s impossible to know exactly what you changed and what you kept constant from your script (unless you tell us for example what numbers were explicitly changed).

Thirdly, how do you know the method you have chosen is a valid method for calculating bulk properties? Are there other papers that have successfully used this method?

3

Hi srtee, many thanks for your reply!

  1. Thanks for pointing out the misformat, I will modify my script accordingly.
  2. For scripts with different box sizes, I only modified one line in the script: region whole block 0 55 0 55 0 55 (change the box size by modifying this line, and keep the others the same). For example: region whole block 0 55 0 55 0 55 sets the box size to 20nm, and then set the box size to 40nm by region whole block 0 111 0 111 0 111.
  3. The method I use to calculate the properties is: the stiffness is the slope of the linear stage, and the yield strength is equal to the stress corresponding to the highest point of the first wave.

Looking forward to your reply, thanks in advance！

4

By “method” I mean using molecular dynamics to simulate the Young modulus and yield strength, in the first place, and then using periodic boundary conditions.

Someone who wants to model a bulk material by just repeating a nanoscale box over and over again can only succeed if their behaviour of interest is dominated by nanoscale phenomena and the material remains homogeneous and isotropic at larger length scales. As a counterexample, soda water has millimeter-sized carbon dioxide bubbles and millimeter-sized bubble-free water domains, so you cannot model the mechanical differences between soda water and normal water (directly) in atomistic MD.

Your copper model with periodic boundary conditions does not correspond to a macroscopic piece of copper and how it would yield under tension. It corresponds to a piece of copper in which, whenever there is a lattice dislocation, that lattice dislocation magically appears as a lattice of regularly-spaced dislocations with a spatial density of hundreds per square millimeter, as a result of the PBC.

That is why I am asking if someone else has done this before. It’s not a crazy idea but it’s probably not a new idea, and I’m sure plenty of people have made mistakes before. You should try to look through the previous literature so you can learn from their mistakes instead of repeating them.

5

Hi srtee,

Thank you so much for your reply. Now that I understand what you mean, I’ll try to search if there are some literatures others have done this.

The reason I did these simulations was to see the effect of box size on mechanical properties (when PBC is applied). What I predicted before doing these simulations was that the mechanical properties were consistent (or very close) or gradually converged as the box size increased (at least in nanoscale), but I found that the mechanical properties gradually increased with the box size, which was unexpected and unexplainable to me. That’s why I’m here to ask for help.

Thank you again, I’ll do what you suggest!

6

I am trying to address the same issue with LAMMPS right now. Were you able to identify a possible way forward?
Thanks!